两点之间的距离公式VIP免费

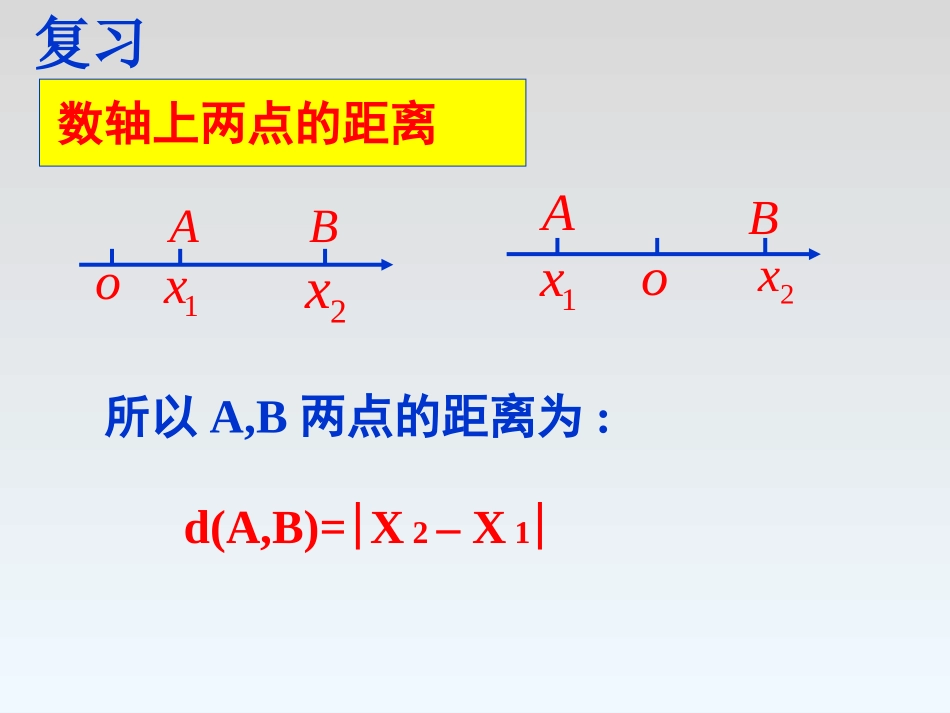
3.3.2两点的距离公式数轴上两点的距离所以A,B两点的距离为:d(A,B)=X2–X11x2xABoo1x2xAB复习合作探究（一）：两点间的距离公式在平面直角坐标系中，已知两点的坐标，怎样来计算这两点之间的距离呢？思考1我们先寻求原点与任意一点之间距离的计算方法yxA,AO,两点之间的距离通常用两点之间的距离通常用ddOAOA表示。0,0O在平面直角坐标系中，已知点A(x，y)，原点O和点A的距离dOA是多少呢？dOA=当A点不在坐标轴上时：A1xyoA(x，y)yxyxoAAA当当AA点在坐标轴上时这一公式点在坐标轴上时这一公式也成立吗？也成立吗？2211,,,yxByxA一般地，已知平面上两点A(x1，y1)和B(x2，y2)，利用上述方法求点A和B的距离222121(,)||()()dABABxxyyA1yxoB(x2，y2)A(x1，y1)B1B2A2显然，当AB平行于坐标轴或在坐标轴上时，公式仍然成立。c【例1】已知A（2、-4）、B（-2，3）.求dAB题型分类举例与练习做p106练习1【例2】已知：点A(1，2)，B(3，4)，C(5，0)求证：三角形ABC是等腰三角形。证明：因为dAB=dAC=dCB=即|AC|=|BC|且三点不共线所以，三角形ABC为等腰三角形。824132220201-52220403522例题分析例题分析.|||,|||,),7,2(),2,1(3的值并求得使轴上求一点在已知点例PAPBPAPxBA2.已知点P(a,2),Q(-2,-3),M(1,1),且|PQ|=|PM|,求a的值。练习练习1.已知A（a，-5）,B（0,10）两点的距离等于17，求a的值。xyO(x,y)A(-3,0)B(2,-2)C(5,2)DM【例4】已知:平行四边形ABCD的三个顶点坐标A(-3,0),B(2,-2),C(5,2).求:顶点D的坐标。分析：因为平行四边形的两条对角线中点相同,所以它们的中点的坐标也相同.解：设D点的坐标为(x,y).则25322x22022y解得x=0y=4∴D(0,4)【例4】已知,求证.22222ADABBDACABCD证明：取证明：取AA为坐标原点，为坐标原点，ABAB所在直线为所在直线为XX轴轴建立平面直角坐标系，依据平行四边建立平面直角坐标系，依据平行四边形的性质可设点形的性质可设点AA，，BB，，CC，，DD的坐标为的坐标为.,,,,0,,0,0cabDcbCaBAxyA(0,0)B(a,0)C(b,c)D(b-a,c)OxOy,22aAB,222cabAD,222cbAC所以所以,422422222abcbaBDAC2222cabBD.22222ADABBDAC所以所以xyA(0,0)B(a,0)C(b,c)D(b-a,c)O,2222222abcbaADAB),22(2222abcba该题用的方法----坐标法。可以将几何问题转化为代数问题。1.两点间的距离公式；2.中点坐标公式二、坐标法——将几何问题转化为代数问题。222121(,)||()()dABABxxyy221xxx221yyy