利用勾股定理求解几何体的最短路线长VIP免费

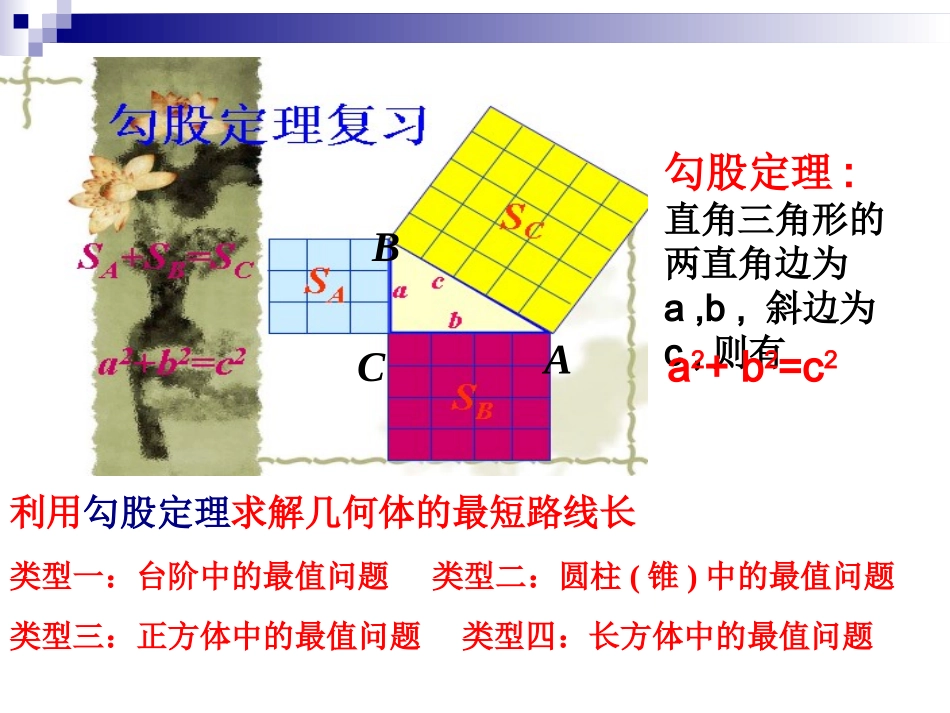
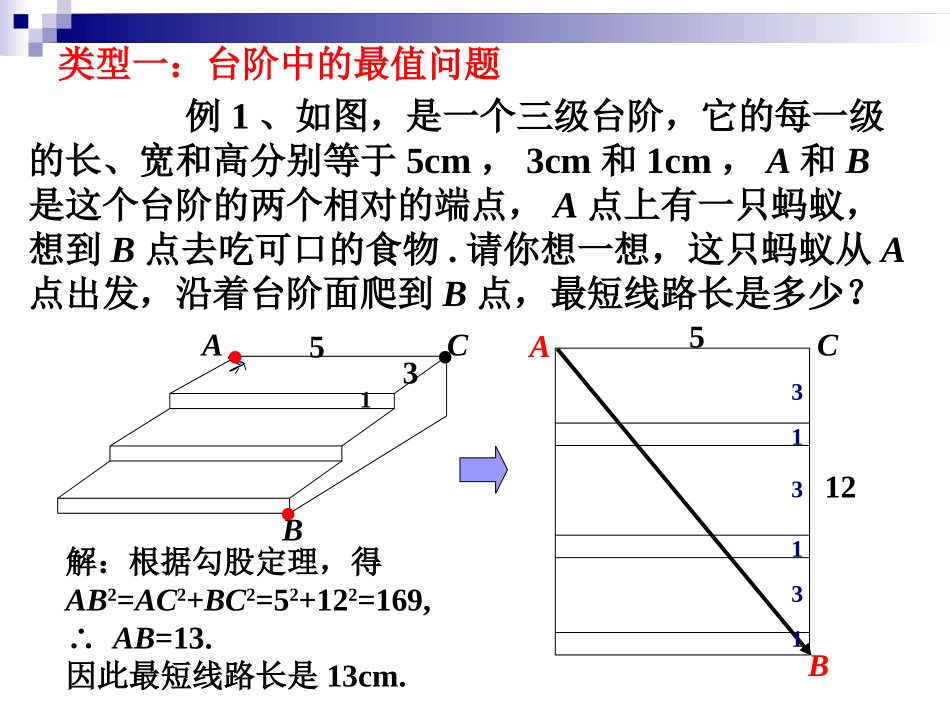
利用勾股定理求解几何体的最短路线长济源市实验中学李登新人教版八年级下册勾股定理:直角三角形的两直角边为a,b,斜边为c,则有a2+b2=c2ACB类型一：台阶中的最值问题类型二：圆柱(锥)中的最值问题类型三：正方体中的最值问题类型四：长方体中的最值问题利用勾股定理求解几何体的最短路线长例1、如图，是一个三级台阶，它的每一级的长、宽和高分别等于5cm，3cm和1cm，A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物.请你想一想，这只蚂蚁从A点出发，沿着台阶面爬到B点，最短线路长是多少？BAABC531512类型一：台阶中的最值问题解：根据勾股定理，得AB2=AC2+BC2=52+122=169,∴AB=13.因此最短线路长是13cm.C...133311类型二：圆柱(锥)中的最值问题例2、如图，有一圆柱形油罐底面圆的周长为24m，高为6m，一只老鼠从距底面1m的A处爬行到对角B处吃食物，它爬行的最短路线长为多少？AB分析：由于老鼠是沿着圆柱的表面爬行的，因此要需把圆柱展开成平面图形.BAC根据两点之间线段最短，可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处，则AB长为最短路线长.解：AC=6–1=5，BC=24×1/2=12，由勾股定理得AB2=AC2+BC2=169,∴AB=13(m).1246因此爬行的最短路线长为13m.类型三：正方体中的最值问题例3、如图，边长为1的正方体中，一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是（）.（A）3（B）（C）2（D）1AB分析：由于蚂蚁是沿正方体的外表面爬行的，因此需把正方体展开成平面图形（如图）.C由勾股定理,得AB2=AC2+BC2=5,∴AB=55FED.21ABCDEFB例4:如图，在长30cm、宽50cm、高40cm的木箱中，如果在箱内的A处有一只昆虫，它沿着箱壁爬行到B处，至少要爬多远？C1CDA.B.305040D1A1B1类型四：长方体中的最值问题CDA.B.3050408000408022ABD1B1C1A1305040ADCBD1A1图1CCDA.B.3040509000903022ABA1D1C1B1AD1BD图②A1B1304050CCDA.B.图③50ADCB40303040507400705022ABD1D1C1C1A1B1C1CDA.B.305040D1A1B1因此，昆虫至少要爬行cm.800090007400＞＞7400如图，一只蚂蚁从实心长方体的顶点A出发，沿长方体的表面爬到对角顶点C1处（三条棱长如图所示），问怎样走路线最短？最短路线长为多少？ABA1B1DCD1C1214分析:根据题意分析蚂蚁爬行的路线有三种情况(如图①②③)D1①ABDCC1421AC1=√42+32=√25;②ABB1CA1C1412AC1=√62+12=√37;AB1D1DA1C1③412AC1=√52+22=√29.由勾股定理，可求得三个图中爬行的路线AC1.练习：因此，可以得到图1中爬行的路线AC1最短，最短路线长为5.把几何体适当展开成平面图形，根据“两点之间线段最短”，或点到直线时“垂线段最短”等性质，利用勾股定理可求解几何体中的最短路线长问题。方法小结：