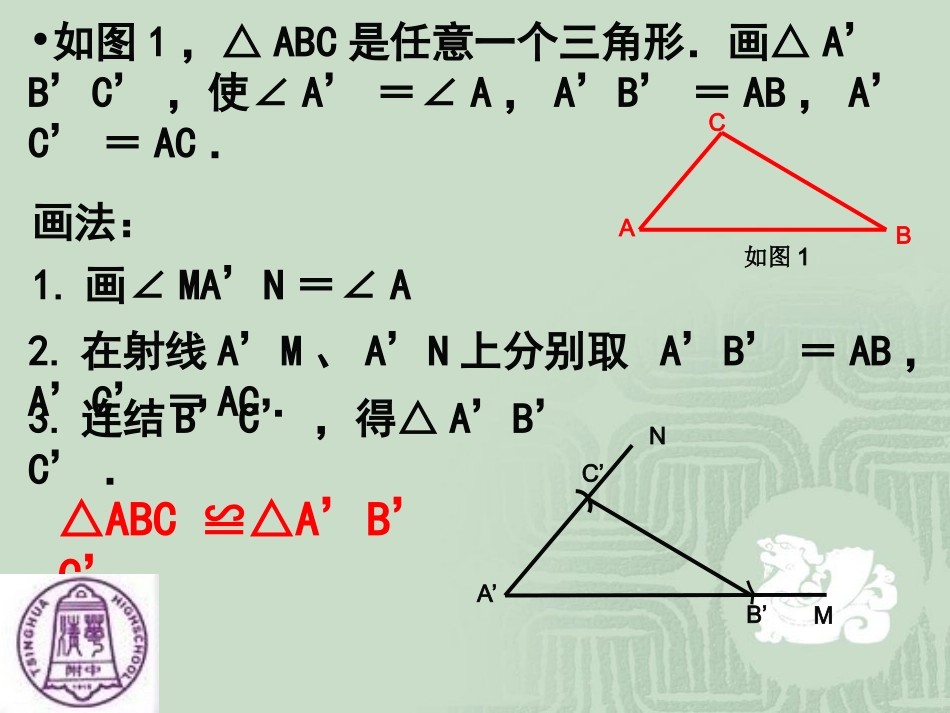
13.2三角形全等的条件•如图1,△ABC是任意一个三角形.画△A’B’C’,使∠A’=∠A,A’B’=AB,A’C’=AC.3.连结B’C’,得△A’B’C’.CABA’MN如图1C’B’2.在射线A’M、A’N上分别取A’B’=AB,A’C’=AC.画法:1.画∠MA’N=∠A△ABC≌△A’B’C’二、“SAS”判定2、两边和它们的夹角对应相等的两个三角形全等。简称“边角边”(SAS)二、“SAS”判定2、两边和它们的夹角对应相等的两个三角形全等。简称“边角边”(SAS)例5、如图,AC=AD,∠CAB=DAB∠,求证:△ACBADB≌△ABCD二、“SAS”例6、如图,ADBC∥,AD=CB,AE=CF,求证:BE=DFABCDEF二、“SAS”例7、如图,已知EBAD⊥于B,FCAD⊥于C,且EB=FC,AB=CD,求证:E=FEFABCD二、“SAS”例8、AB=CD,BE=DF,∠B=D∠,求证:(1)AF=CE,(2)AFCE∥ABCDEF二、“SAS”3、如图,在△ABC中,延长AC边上的中线BD到F,使DF=BD,延长AB边上的中线CE到G,使EG=CE,求证:AF=AG练习ABCDEFG二、“SAS”4、如图,在AB、AC上各取一点E、D,使AE=AD,连结BD、CE相交于点O,连结AO,∠1=2∠,求证:∠B=C∠练习ABCDEO12二、“SAS”由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗?为什么?ABCA’B’C’思考以3cm、4cm为三角形的两边,长度3cm的边所对的角为45°,情况又怎样?动手画一画,你发现了什么?ABC3cm4cm45°3cm结论:两边及其一边所对的角相等,两个三角形不一定全等做一做MMB’步骤:1.画一线段AC,使它等于4cm2.画∠CAM=45°3.以C为圆心,3cm长为半径画弧,交AM于点B4.连结CB△ABC就是所求做的三角形显然:△ABC与△AB’C不全等和B’、CB’与△AB’C二、“SAS”