281锐角三角函数2VIP免费

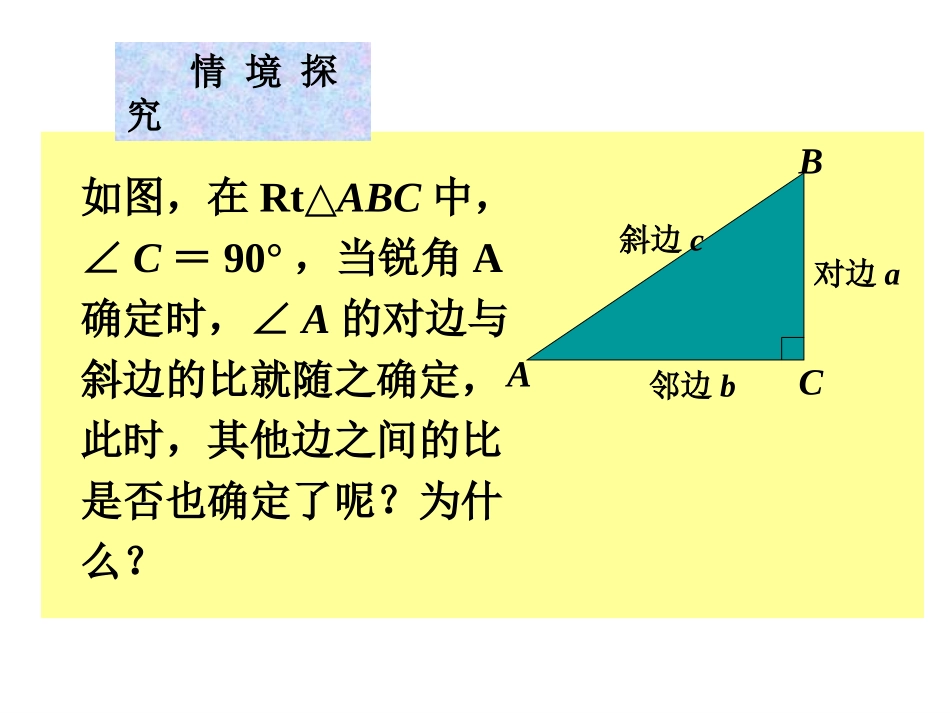
28.1锐角三角函数（2）1、sinA是在直角三角形中定义的，∠A是锐角2、sinA是一个比值（数值）。3、sinA的大小只与∠A的大小有关，而与直角三角形的边长无关。如图：在RtABC△中，∠C＝90°，sin30°=2122sin45°=特殊角的正弦函数值正弦复习caAsinA斜边的对边如图，在Rt△ABC中，∠C＝90°，当锐角A确定时，∠A的对边与斜边的比就随之确定，此时，其他边之间的比是否也确定了呢？为什么？ABC邻边b对边a斜边c情境探究当锐角A的大小确定时，∠A的邻边与斜边的比、∠A的对边与邻边的比也分别是确定的，我们把∠A的邻边与斜边的比叫做∠A的余弦（cosine），记作cosA，即cbAA斜边的邻边cos把∠A的对边与邻边的比叫做∠A的正切（tangent），记作tanA，即baAAA的邻边的对边tan锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数．情境探究例2如图，在Rt△ABC中，∠C＝90°，BC＝6，sinA＝，求cosA、tanB的值．53ABC6例题示范1.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值．练习ABC13122.在Rt△ABC中，如果各边长都扩大2倍，那么锐角A的正弦值、余弦值和正切值有什么变化？ABCABC练习3.如图，在Rt△ABC中，∠C＝90°，AC＝8，tanA＝，求：sinA、cosB的值．43ABC8练习应用举例1、在RtABC△中，∠C＝90°，求∠A的三角函数值。①a=9，b=12②a=5，b=122、在△ABC中，AB=AC＝4，BC=6，求∠B的三角函数值。3、已知∠A为锐角，sinA＝，求cosA、tanA的值。17151、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值（）A.扩大100倍B.缩小100倍C.不变D.不能确定ABC┌C试一试：试一试：2、如图，∠ACB=90°，CD⊥AB于点D，指出∠A和∠B的对边、邻边。ABCD(1)tanA==AC()CD()(2)tanB==BC()CD()BCADACBD=ac的斜边的对边AAsinA=小结回顾在Rt△ABC中=bc的斜边的邻边AAcosA==ab的邻边的对边AAtanA=定义中应该注意的几个问题:1、sinA、cosA、tanA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)。2、sinA、cosA、tanA是一个比值（数值）。3、sinA、cosA、tanA的大小只与∠A的大小有关，而与直角三角形的边长无关。小结回顾