函数的极值课件VIP免费

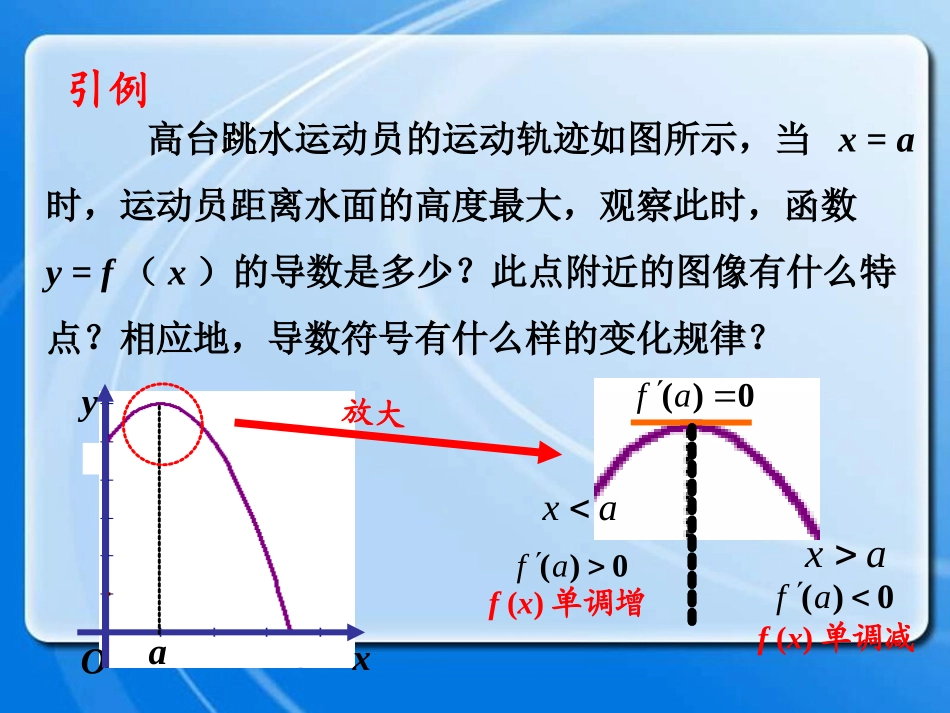
解得的单调减区间。)(xf0)(xf＊用导数求函数的单调区间：（1）求，并判断的符号；)(xf)(xf（2）解不等式得的单调增区间；0)(xf)(xf＊求函数的单调性：（1）定义法；（2）导数法。复习回顾高台跳水运动员的运动轨迹如图所示，当x=a时，运动员距离水面的高度最大，观察此时，函数y=f（x）的导数是多少？此点附近的图像有什么特点？相应地，导数符号有什么样的变化规律？引例0)(afxyOa0)(aff(x)单调增0)(aff(x)单调减放大axax当x在a附近从小到大经过a时，先正后负，且连续变化,于是有=0。)(xf)(xf)(xfy=f(x)在x=a的函数值f(a)比它在这点附近其它点的函数值都大，；而且在x=a附近的左侧，右侧，则f(a)叫做极大值，a叫极大值点。类似地，可定义极小值点。0)(af0)(af0)(af给出定义：可以发现：定义，函数y=f(x)在任何一点的函数值都不大于点的函数值，则称点为函数y=f(x)的极大值点，其函数值为函数的极大值。)(0xf),(0bax0x0x)(xfOxyab0x)(xfOxyab0x极大值与极小值统称极值，极大值点与极小值点统称为极值点。，函数y=f(x)在任何一点的函数值都不小于点的函数值，则称点为函数y=f(x)的极小值点，其函数值为函数的极小值。)(0xf),(0bax0x0x同理，练习是在内的极大值点：0x)(xfy),(ba是在内的极小值点：0x)(xfy),(ba“左正右负极大值”“左负右正极小值”概括例1求函数的极值点。53632)(23xxxxf例2求函数的极值。133)(3xxxf解析解析求极值的步骤：1.求导数；)(xf2.解方程；0)(xf3.对于方程的每一个解，分析在左右两侧的符号，确定极值点：在两侧若的符号)(xf0)(xf0x0x)(xf0x（1）“左正右负”，则为极大值点；0x（2）“左负右正”，则为极小值点；0x（3）相同，则不是极值点；0x1.下列函数存在极值的是（）332.2..1.xyDyCxyBxyA2.判断下列函数是否有极值，若有，请求出极值；若无，请说明理由。593)2(16128)1(2323xxxyxxxy左右两侧，导数符号相同。21无10)1()(fxf极大值22)3()(fxf极小值B动手做一做＊求极值的步骤：1.求导数；)(xf2.解方程；0)(xf3.对于方程的每一个解，分析在左右两侧的符号，确定极值点，求极值。)(xf0)(xf0x0x“左正右负极大值”“左负右正极小值”＊规律：小结结束观察函数的图像，回答：（1）的极大值点有___个，分别是_________________；（2）的极小值点有___个，分别是_________________。)(x)(x)(x26.51217-1-3.5-6)(xxy11-3.56.5×正确么？4-6、-1、172、1236.5-3.5极大（小）值点不是最大（小）值点，并非只有一个动手做一做注意：（1）极值是在某个小区域内的局部性质，在整个定义域内，可以有很多个极小值和极大值，在某点的极小值可能大于另一点的极大值，即极大值不一定比极小值大，极小值也不一定比极大值小。定义理解（3）函数的极值点的分布是有规律的。相邻的两个极大值点之间必有一个极小值点，相邻的两个极小值点之间必有一个极大值点。（2）函数的极值点的导数是0，但导数是0的点可能不是极值点。仅当某点处导数为0且其两侧导数符号相反时，此点才是极值点。亦即：y=f(x)在(a，b)内不是单调函数，则在此区间内f(x)有极值。在区间上单调的函数没有极值。概括分析：由总结可知，极值点是导数为零的点，故需解方程，再判断的符号。满足规律：“左正右负极大值”、“左负右正极小值”。0)(xf)(xf解：3666)(2xxxf由可得0)(xf3,221xx++-00↗↗↘极大极小将-2和3代入，即可算得极值。)(xfy极值又是多少？如何计算？从表中可以直观的发现：-2是函数的极大值点；3是函数的极小值点。例2++-00↗↗↘极大极小解：由可得0)(xf39)(2xxf33,3321xx从表中可以发现：是函数的极大值点；是函数的极小值点，极大、极小值分别为：33333321)33(f3321)33(f133)(3xxxf3333概括