锐角三角函数2VIP免费

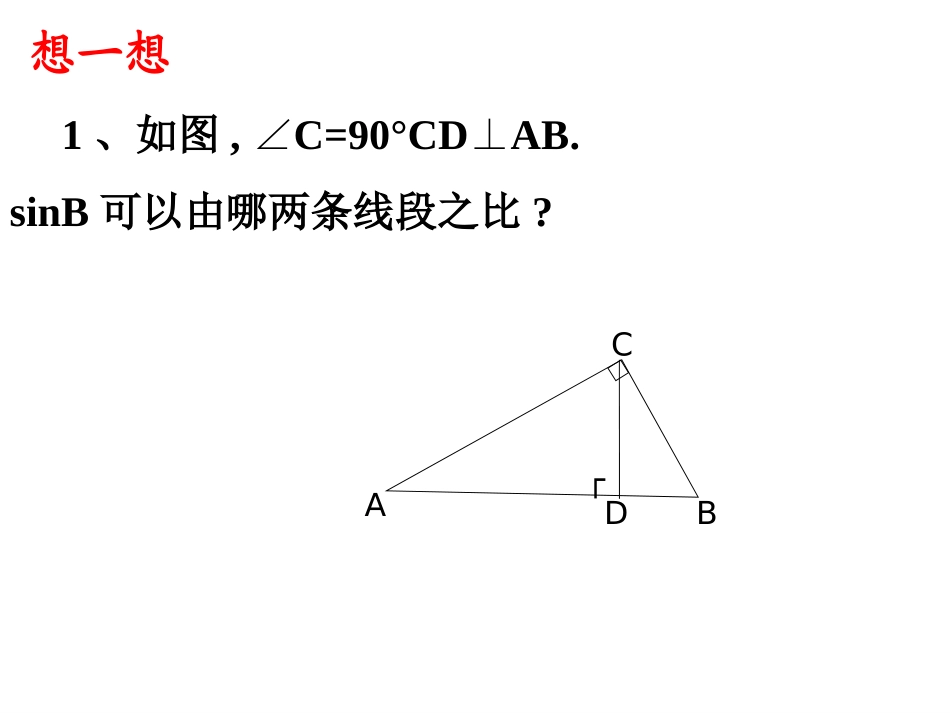
锐角三角函数（2）1、sinA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)。2、sinA是一个比值（数值）。3、sinA的大小只与∠A的大小有关，而与直角三角形的边长无关。如图：在RtABC△中，∠C＝90°，sin30°=2122sin45°=23sin60°=特殊角的正弦函数值正弦复习caAsinA斜边的对边1、如图,C=90°CDAB.∠⊥sinB可以由哪两条线段之比?想一想┌ACBD3、已知在Rt△ABC中,∠C=900,D是BC中点,DE⊥AB,垂足为E,sin∠BDE=,AE=7,求DE的长.ABCDE54当直角三角形的一个锐角的大小确定时，其任意两边的比值都是惟一确定的吗？为什么？探究∟对边a斜边c邻边b我们把∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，即baAAtan的邻边的对边A把∠A的对边与邻边的比叫做∠A的正切，记作tanA，即cbAcos斜边的邻边A在直角三角形中，当锐角A的度数一定时，不管三角形的大小如何，∠A对边与斜边的比及对边与邻边的比是一个固定值。BACA′B′C′任意画RtABC△和RtA′B′C′△，使得∠C=C′=90°∠，∠A=A′=∠α。那么BCAC和B′C′A′C′有什么关系？BCAB和B′C′A′B′，及由于∠C=C′=90°∠，∠A=A′=α∠，所以RtABCRtA′B′C′△∽△，BCAB=B′C′A′B′，BCAC=B′C′A′C′。如图：在RtABC△中，∠C＝90°，∟BACbca斜边对边∠A的对边记作a，∠B的对边记作b，∠C的对边记作c。邻边对于锐角A的每一个值，sinA有唯一的值和它对应，所以sinA是A的函数，同样地，cosA，tanA也是A的函数。锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数。例如图，在RtABC△中，∠C=90°，BC=6，sinA=，求cosA，tanB的值。ABC6解：∵sinA=，∴AB==6×=10，BCABBCsinA2222610BCAB34BCAC又AC==8，∴cosA=，tanB=3554ABAC53应用举例1、在RtABC△中，∠C＝90°，求∠A的三角函数值。①a=9b=12②a=9b=122、在△ABC中，AB=AC＝4，BC=6，求∠B的三角函数值。3、已知∠A为锐角，sinA＝，求cosA、tanA的值。17154、如图，在RtABC△中，∠C=90°，AC=8，tanA=，求sinA，cosB的值。43BAC1、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值（）A.扩大100倍B.缩小100倍C.不变D.不能确定ABC┌C试一试：试一试：2、下图中∠ACB=90°，CD⊥AB,垂足为D。指出∠A和∠B的对边、邻边。ABCD(1)tanA==AC()CD()(2)tanB==BC()CD()BCADACBD•直角三角形ABC中，∠C=900，CDAB⊥于D，求证：CD2=AD×BD•AC2=AD×AB•BC2=BD×BAADCB正方形ABCD中，CM=DM，BN=3CN，求tanMAN∠MNDCBA如图，AB为直径，BD为弦，弦BC平分∠ABD的外角，CFBD⊥于F，若BD=3BF，求cosACD∠BCDFA=ac的斜边的对边AAsinA=小结回顾在Rt△ABC中=bc的斜边的邻边AAcosA==ab的邻边的对边AAtanA=定义中应该注意的几个问题:回顾小结1、sinA、cosA、tanA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)。2、sinA、cosA、tanA是一个比值（数值）。3、sinA、cosA、tanA的大小只与∠A的大小有关，而与直角三角形的边长无关。