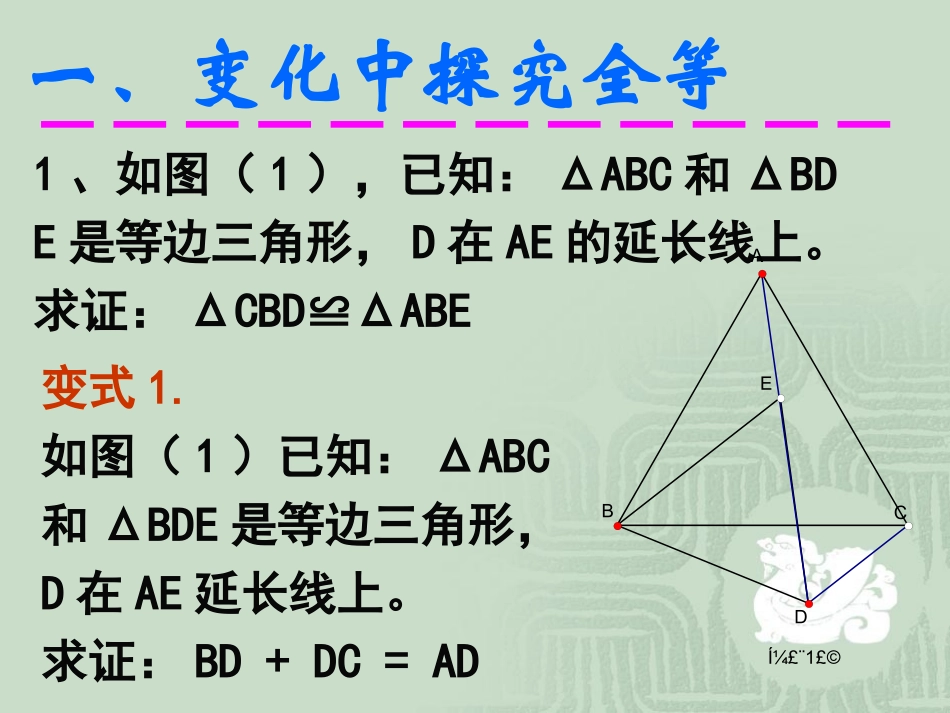
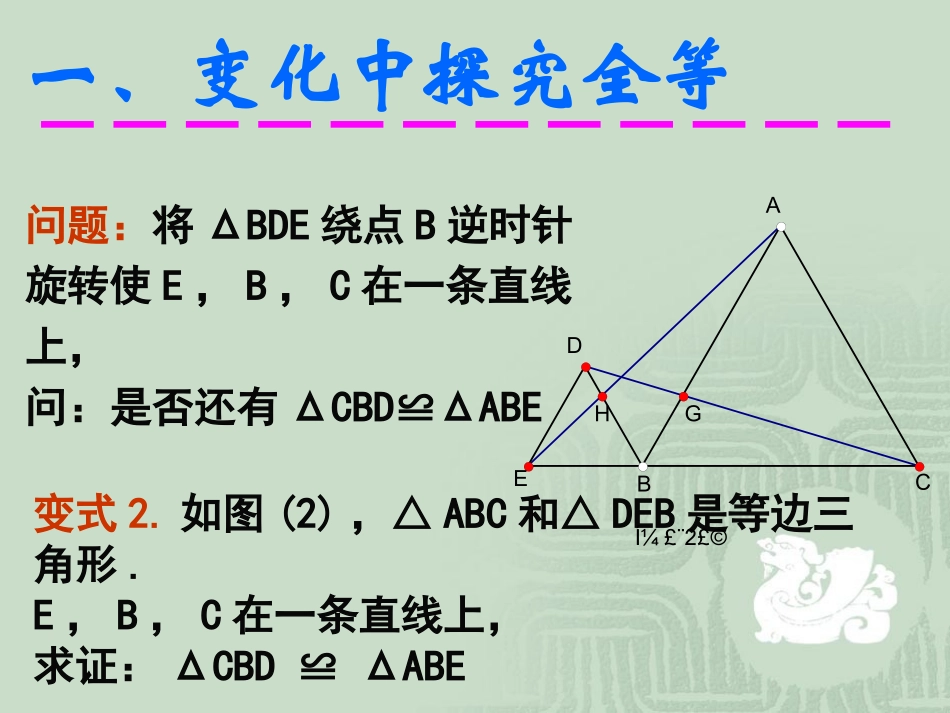
全等三角形复习提高版1、如图(1),已知:ΔABC和ΔBDE是等边三角形,D在AE的延长线上。求证:ΔCBD≌ΔABEͼ£¨1£©ECABD变式1.如图(1)已知:ΔABC和ΔBDE是等边三角形,D在AE延长线上。求证:BD+DC=AD一、变化中探究全等问题:将ΔBDE绕点B逆时针旋转使E,B,C在一条直线上,问:是否还有ΔCBD≌ΔABE变式2.如图(2),△ABC和△DEB是等边三角形.E,B,C在一条直线上,求证:ΔCBD≌ΔABEͼ£¨2£©GHABDEC一、变化中探究全等ͼ£¨2£©GHABDEC变式3.如图(2),△ABC和△DEB等边三角形.E,B,C在一条直线上.求证:BG=BH.一、变化中探究全等2.已知如图:在△ABC中,∠ABC=,H是高AD和BE的点,1).求证:BH=AC.45ACBEDH证明线段相等有两种方法:1.当两条线段在不同三角形上,则证明两个三角形全等.2.当两条线段在同一个三角形,则利用等腰三角形的等角对等边.一、变化中探究全等2.已知如图:在△ABC中,∠ABC=,H是高AD和BE的点,1).求证:BH=AC.45ACBEDH2).若把∠BAC改为钝角,请你按题设要求在钝角三角形ABC中画出该题的图形?ACBEDH一个图形的某些条件变化后,要能分清变与不变的结果,这是解决这一类问题的基本思路.结论BH=AC还成立吗?一、变化中探究全等NMBACEDF3.已知C为AB上一点,△ACN和△BCM是正三角形.(1).求证:AM=BN.(2).求∠AFN的度数.一、变化中探究全等(3).将原题中的正三角形改为正方形,根据上面(1),(2)的启示,能说明AM与BN的位置与数量关系吗?NMBACEDF一个图形的某些条件变化后,要能分清变与不变的结果.一、变化中探究全等NMBACEDFO(4).现以AB所在的直线为X轴,以△ACN的高线NO所在的直线为Y轴建立坐标系,如图所示.B,C的坐标分别是(4,0),(2,0).I)求点M的坐标;II)写出直线AM的函数解析式;III)求出△AFB的面积.D一、变化中探究全等与后续内容可以再综合二、经典集粹三角形ABC中,AB=AC,顶角为100度,BE为底角的角平分线,求证:BC=AE+BE。思考角平分线构造全等+“SSA”反例ABCE二、经典集粹思考构造两次全等如图,已知AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边形ABCDE的面积。BAECD二、经典集粹思考如图,直角梯形ABCD,AD//BC,AD=2,BC=3,等腰直角三角形CDE,CE为斜边,连结AE,求三角形ADE的面积。CBDEA二、经典集粹如图,直角梯形ABCD,AD//BC,AD=2,BC=3,等腰直角三角形CDE,CE为斜边,连结AE,求三角形ADE的面积。CFBDEAHCBDEFA请同学们谈谈这节课的收获!(1)利用全等三角形证明线段相等时,关键要找好背景三角形。(2)一个图形的某些条件变化后,要能分清变与不变的结果,这是解决这一类问题的基本思路。(3)求证线段或角相等转化为证明它们所在的三角形全等。(4)多边形问题转化为三角形解决。