球球的体积课件VIP免费

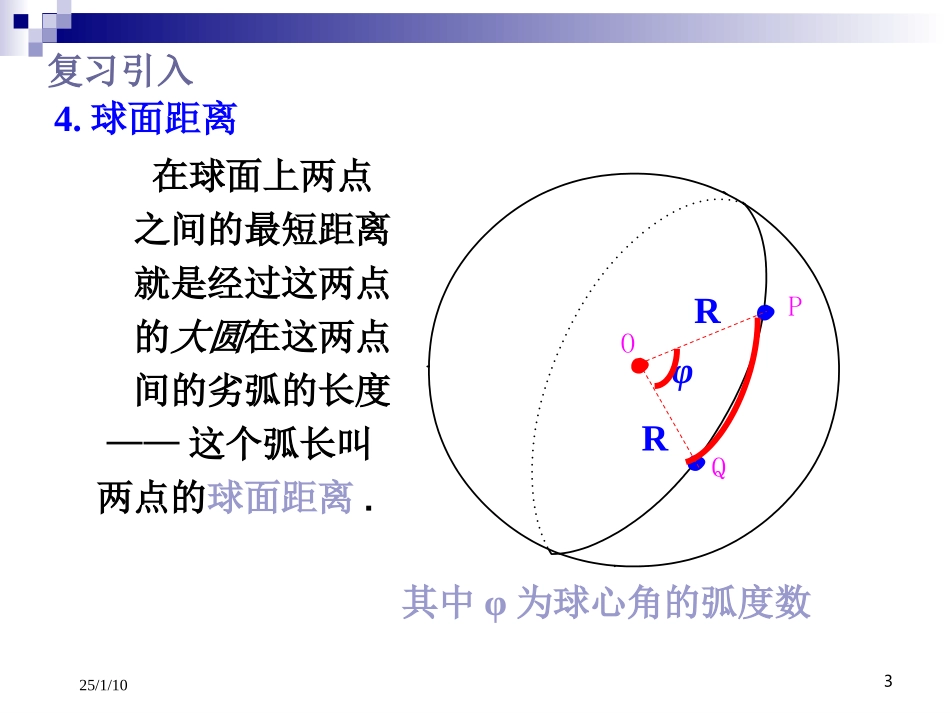
225/1/101.球面、球体的概念（两种定义）？2.球的截面的基本性质？复习引入4.地球的经度纬度－纬线和纬度？cosrR纬地纬3.地球的经度纬度－经线和经度？325/1/10在球面上两点之间的最短距离就是经过这两点的大圆在这两点间的劣弧的长度——这个弧长叫两点的球面距离.OPQRRφ其中φ为球心角的弧度数4.球面距离复习引入425/1/10h实验：排液法测小球的体积复习引入525/1/10h复习引入625/1/10h实验：排液法测小球的体积复习引入725/1/10h实验：排液法测小球的体积复习引入825/1/10h实验：排液法测小球的体积复习引入925/1/10实验：排液法测小球的体积复习引入h1025/1/10实验：排液法测小球的体积复习引入h1125/1/10h实验：排液法测小球的体积复习引入1225/1/10hH小球的体积小球的体积等于等于它排开液体的它排开液体的体积体积曹冲称象实验：排液法测小球的体积复习引入1325/1/10新知识讲解用几何画板演示问题:已知球的半径为R,用R表示球的体积？1425/1/10O新知识讲解1525/1/10i第层“小圆片”下底面的半径：22[(1)],1,2,,.RRiinnirORir(1)Rin问题:已知球的半径为R,用R表示球的体积.新知识讲解1625/1/10问题:已知球的半径为R,用R表示球的体积.新知识讲解1725/1/10AOirO.niinRRri,2,1,)]1([22,21RRr,)(222nRRrA2O2AiOiSO,)2(223nRRr1825/1/10nininRnRrVii,2,1],)1(1[232问题:已知球的半径为R,用R表示球的体积.niinRRri,,2,1,)]1([22nVVVV21半球])1(21[22223nnnnR]6)12()1(1[23nnnnnnR3111[1(1)(2)]6Rnn323nnR当很大很大时3V.R球43＝新知识讲解1925/1/103V.R球＝球43的体积：推导球的体积的基本思路：分割求近似和逼近（求极限）化为标准和（公式）5.球的体积新知识讲解2025/1/101.球的直径伸长为原来的2倍，计算体积变为原来的倍.2.一个正方体的顶点都在球面上，它的棱长为4cm，求这个球的体积.83323cm答案：CBB'ADO''C'OO'D'A'正方体的外接球课堂练习2125/1/10第一步：分割O球面被分割成n个网格，表面积分别为：nSSSS...321，，则球的表面积：nSSSSS...321则球的体积为：设“小锥体”的体积为：iViVnVVVVV...321iSO6.球的表面积新知识讲解2225/1/10O第二步：求近似和Oih由第一步得：nVVVVV...321nnhShShShSV31313131332211...iiihSV31iSiV6.球的表面积新知识讲解2325/1/10第三步：化为准确和1133iiiiVShSR如果网格分的越细,则:RSRSRSRSVni3131313132...RSSSSSRni313132)...(①由①②得334RV②球的体积:球面2S4πRiSiVih的值就趋向于球的半径RRihiSOiV“小锥体”就越接近小棱锥.6.球的表面积新知识讲解2425/1/10例如图正方体ABCD-A′B′C′D′的棱长为a,它的各个顶点都在球O的球面上，问球O的表面积.分析：正方体内接于球，则由球和正方体都是中心对称图形可知，它们中心重合，则正方体对角线与球的直径相等。解：22222:223(2)(2),243RtACCACRACaRaaRaSRa中，得：关键：找正方体的棱长a与球半径R之间的关系CBB'ADO''C'OO'D'A'例题讲解2525/1/10(1)若球的表面积变为原来的2倍,则半径变为原来的____倍.(2)若球的半径变为原来的2倍，则表面积变为原来的____倍.(3)若两球表面积之比为1:2，则其体积之比是________.(4)若两球体积之比是1:2，则其表面积之比是_________.2422:134:1课堂练习2625/1/101.两种方法:化整为零的思想方法和“分割,求和,取极限”的数学方法.2.一个观点:在一定条件下,化曲为直的辨证观点.3.一个公式:半径为R的球的体积是334RV4.利用“分割-求近似和-化为准确和”的数学方法推出了球的表面积公式：24πRS2725/1/10本讲到此结束，请同学们课后再做好复习.谢谢！作业：习题9.106，7奎屯王新敞新疆·2007·新疆奎屯wxckt@126.com特级教师http://wxc.833200.com王新敞源头学子小屋