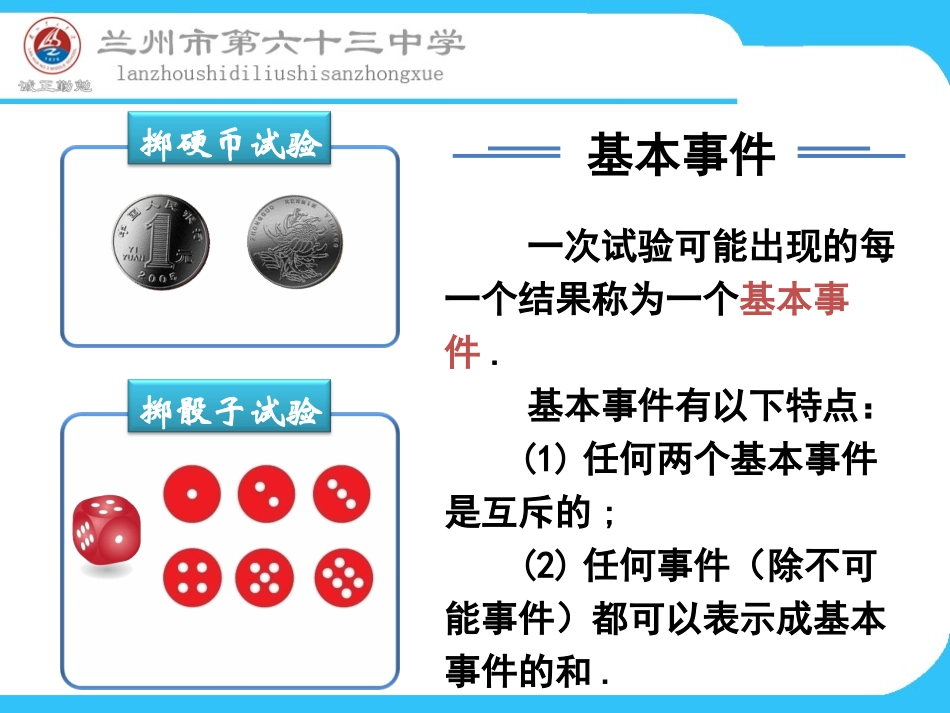
普通高中课程标准实验教科书·数学必修三(人民教育出版社A版)掷硬币试验掷骰子试验一次试验可能出现的每一个结果称为一个基本事件.基本事件有以下特点:(1)任何两个基本事件是互斥的;(2)任何事件(除不可能事件)都可以表示成基本事件的和.基本事件阅读课本P126—P127例2前,回答以下两个问题:(1)什么是古典概型?(2)古典概型的概率计算公式.上述试验的共同特点是:(1)试验中所有可能出现的基本事件只有有限个;(有限性)(2)每个基本事件出现的可能性相等.(等可能性)我们将具有这两个特点的概率模型称为古典概率模型,简称古典概型.根据上述两则模拟试验,可以概括总结出,古典概型计算任何事件的概率计算公式为:AA所包含的基本事件的个数()=基本事件的总数P在使用古典概型的概率公式时,应该注意什么?(1)要判断该概率模型是不是古典概型;(2)要找出随机事件A包含的基本事件的个数和试验中基本事件的总数.课堂合作探究问题1:向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?有限性等可能性问题2:某同学随机地向一靶心进行射击,这一试验的结果只有有限个:“命中10环”、“命中9环”、“命中8环”、“命中7环”、“命中6环”、“命中5环”和“不中环”.你认为这是古典概型吗?为什么?1099998888777766665555有限性等可能性问题导学一、基本事件的计数问题活动与探究1(1)从集合{1,2,3,4}中任取两个数字(可重复)组成平面直角坐标系中某点的坐标,则有多少个基本事件,其中纵坐标大于横坐标的有几个基本事件?(2)从甲、乙、丙、丁四位同学中任选两人参加演讲比赛,共有多少个基本事件,其中甲同学参加演讲比赛的有几个基本事件?思路分析:用列举法列出所有的基本事件,再确定个数.解:(1)所有可能的基本事件有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4),共16个.其中纵坐标大于横坐标的有(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),共6个基本事件.(2)所有的基本事件有(甲,乙),(甲,丙),(甲,丁),(乙,丙),(乙,丁),(丙,丁),共6个.其中甲参加的有(甲,乙),(甲,丙),(甲,丁),共3个基本事件.(1)在求基本事件时,一定要按规律去写,这样不容易漏写.(2)确定基本事件是否与顺序有关.(3)写基本事件时,主要用列举法,具体写时可用列表法或树状图法.例1单选题是标准化考试中常用的题型,一般是从A,B,C,D四个选项中选择一个正确答案.如果考生掌握了考查的内容,他可以选择唯一正确的答案.假设考生不会做,他随机地选择一个答案,问他答对的概率是多少?41(基本事件的总数事件的个数“答对”所包含的基本“答对”)P二、古典概型的概率求法活动与探究2假设有20道单选题,如果有一个考生答对了17道题,他是随机选择的可能性大,还是他掌握了一定的知识的可能性大?应用极大似然法的思想,假设他每道题都是随机选择答案的,可以估计出他答对17道题的概率为11171082.541可以发现这个概率是很小的;如果掌握了一定的知识,绝大多数的题他是会做的,那么他答对17道题的概率会比较大,所以他应该掌握了一定的知识.答:他应该掌握了一定的知识.求古典概型概率的计算步骤是:(1)算出基本事件的总数n;(2)算出事件A包含的基本事件的个数m;(3)算出事件A的概率P(A)=𝑚𝑛.例2同时掷两个骰子,求:(1)向上的点数均为3的概率.(2)向上的点数和为5的概率.(3)向上的点数和为偶数的概率.112345621234563123456412345651234566123456解:同时掷两个骰子的基本事件共有36个.(1)求向上的点数均为3的概率.因此,向上点数均为3的概率为.P(A)=3611234561(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)2(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)3(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)4(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)5(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)6(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)解:同时掷两个骰子的基本事件共有36个.设向上点数均为3为事件A.其中,事件A包含(3,3)1个基本事件.1234561(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)2(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)3(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)4(1,4)(2...