点到直线的距离两平行线间的距离VIP免费

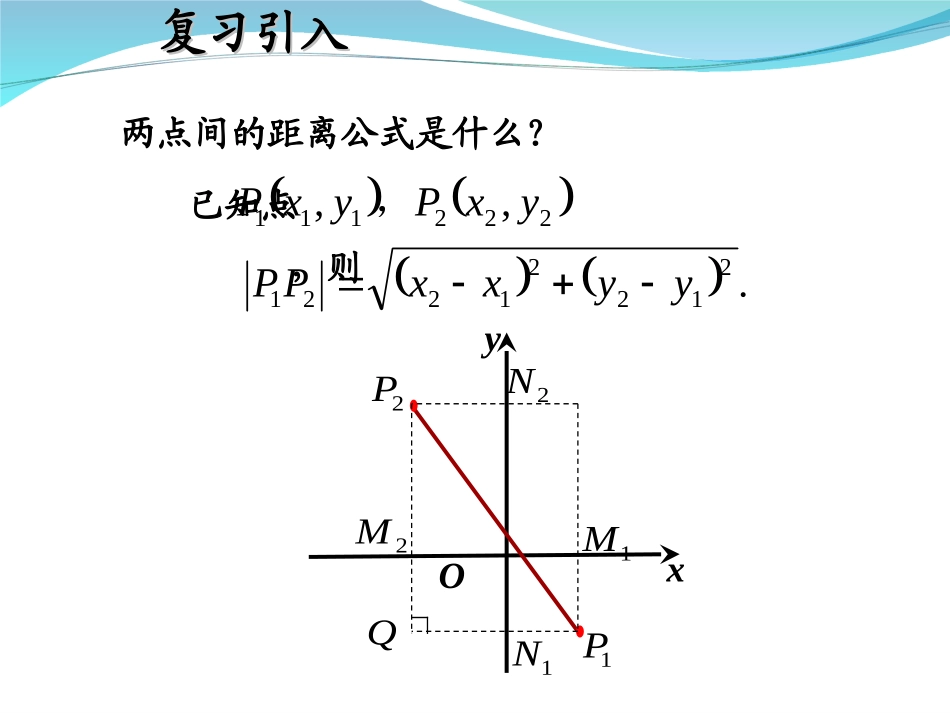
3.3.3《点到直线的距离》3.3.4《两平行线间的距离》教学目标使学生了解点到直线距离公式的推导，能记住点到直线距离的公式，并会应用公式解题。教学重点：点到直线距离的公式及其应用。教学难点：点到直线的距离公式的推导。两点间的距离公式是什么？已知点，则222111,,yxPyxP，.21221221yyxxPPxyO1P2P1M2NQ2M1N复习引入复习引入已知点，直线，如何求点到直线的距离？000,yxP0:CByAxl0Pl点到直线的距离，是指从点到直线的垂线段的长度，其中是垂足．0P0PllQP0QxyO0PlQ引入新课引入新课xyO0PlQ试一试，你能求出吗？QP0点到直线的距离点到直线的距离点到直线距离公式xyP0(x0,y0)O|y0||x0|x0y0点到直线距离公式xyP0(x0,y0)O|x1-x0||y1-y0|x0y01yyy11xxx1思路一：直接法直线的方程l直线的斜率lQPl0直线的方程l直线的方程QP0交点QP0点之间的距离（到的距离）QP、00Pl点的坐标0P直线的斜率QP0点的坐标0P点的坐标Q两点间距离公式xyO0PlQ点到直线的距离点到直线的距离思路简单运算繁琐回忆建立两点间的距离公式的过程．xyO1P2P1M2NQ2M1N首先求出两条与坐标轴平行的线段的长度，然后利用勾股定理求出这两点间的距离（斜边长）．点到直线的距离点到直线的距离思路二：间接法xyO0PlQ面积法求出求出求出利用勾股定理求出点到直线的距离点到直线的距离||0RP||0SP||RS||0QPSR求出点的坐标R求出点的坐标S已知点，直线，求点到直线的距离？000,yxP0:CByAxl0PlxO0PlQdSRy如图，设0,0AB都相交，则直线与轴和轴yxlR的坐标为00(,)ByCyA的坐标为S00(,)AxCxB则直线的方程为0PR0yy直线的方程为0PS0xx于是有00000AxByCByCPRxAA00000AxByCAxCPSyBB22220000ABRSPRPSAxByCAB设0,PQd由三角形的面积公式得00dRSPRPS于是得000022PRPSAxByCdRSABxyO0PlQ点到直线的距离：000,yxP0:CByAxl2200BACByAxd点到直线的距离点到直线的距离当A=0或B=0，此公式也成立。注意例1求点到直线的距离．210，P23:xl解：350321322d思考：还有其他解法吗？典型例题典型例题例题分析例题分析例6:已知点A(1,3),B(3,1),C(-1,0),求的面积ABCxyOABCh12:,,||ABCABhSABh解如图设边上的高为则22)31()13(||22AB的距离到就是点边上的高ABChAB041313-13-yyxxAB即边所在直线的方程为2511|401|22h5252221,ABCS因此yxol2l1两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.两条平行直线间的距离：两条平行直线间的距离：QP例2求平行线2x-7y+8=0与2x-7y-6=0的距离。Oyxl2:2x-7y-6=0l1:2x-7y+8=0P(3,0)两平行线间的距离处处相等在l2上任取一点，例如P(3,0)P到l1的距离等于l1与l2的距离5353145314)7(28073222d直线到直线的距离转化为点到直线的距离两条平行直线间的距离：两条平行直线间的距离：Oyxl2l1PQ任意两条平行直线都可以写成如下形式：l1:Ax+By+C1=0l2:Ax+By+C2=0PQ2212BACC两条平行直线间的距离：两条平行直线间的距离：1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;2.两平行线3x+4y=10和6x+8y=0的距离是____.练习练习332.两条平行线Ax+By+C1=0与Ax+By+C2=0的距离是2221BAC-Cd+=2200BACByAxd+++=1.平面内一点P(x0,y0)到直线Ax+By+C=0的距离公式是当A=0或B=0时,公式仍然成立.小结小结练习P1081，2作业P1108,9