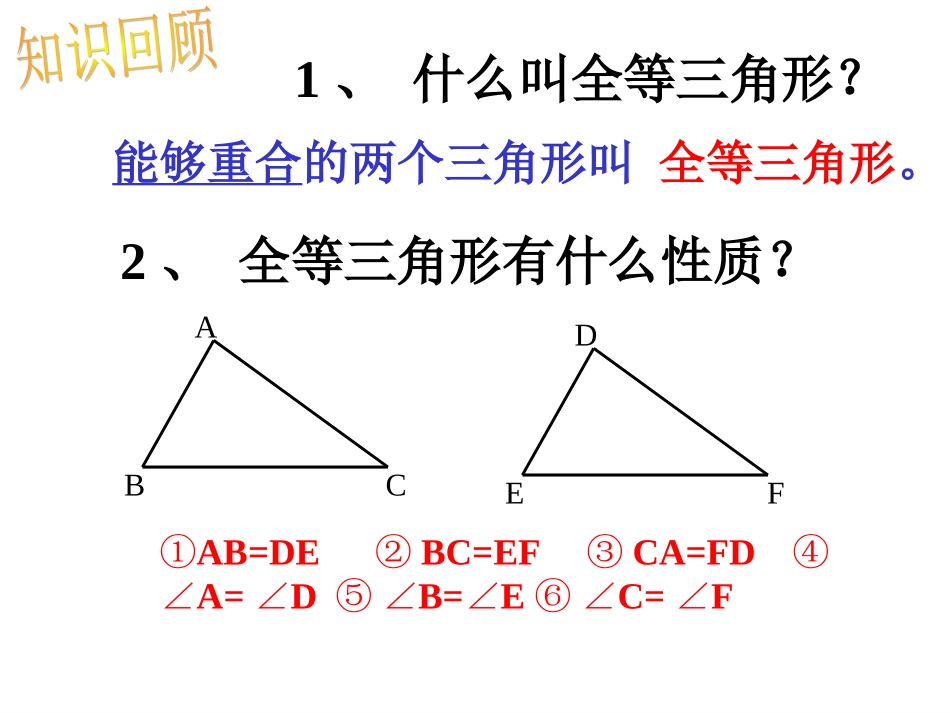
13.2三角形全等的条件(一)①AB=DEBC=EFCA=FD②③④A=DB=EC=F∠∠⑤∠∠⑥∠∠ABCDEF1、什么叫全等三角形?能够重合的两个三角形叫全等三角形。2、全等三角形有什么性质?寻找对应元素的规律(1)有公共边的,公共边是对应边;(2)有公共角的,公共角是对应角;(3)有对顶角的,对顶角是对应角;(4)两个全等三角形最大的边是对应边,最小的边是对应边;(5)两个全等三角形最大的角是对应角,最小的角是对应角;情境问题情境问题::小明家的衣橱上镶有两块小明家的衣橱上镶有两块全等的三角形玻璃装饰物全等的三角形玻璃装饰物,,其中一块被打碎了其中一块被打碎了,,妈妈让妈妈让小明到玻璃店配一块回来小明到玻璃店配一块回来,,请你说说小明该怎么办请你说说小明该怎么办??1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:60°60°60°探究:可以发现按这些条件画的三角形都不能保证一定全等2.给出两个条件:①一边一内角:②两内角:③两边:30°30°30°30°30°50°50°2cm2cm4cm4cm可以发现按这些条件画的三角形都不能保证一定全等。三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。已知三角形三条边分别是4cm,5cm,7cm,画出这个三角形,把所画的三角形分别剪下来,并与同伴比一比,发现什么?思考:你能用“边边边”解释三角形具有稳定性吗?判断两个三角形全等的推理过程,叫做证明三角形全等。ABCDEF用数学语言表述:在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFCA=FD例1.如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。求证:△ABDACD≌△分析:要证明△ABDACD≌△,首先看这两个三角形的三条边是否对应相等。结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程。①准备条件:证全等时要用的间接条件要先证好;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤:已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),要用“边边边”证明△ABCFDE≌△,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?解:要证明△ABCFDE≌△,还应该有AB=DF这个条件∵DB是AB与DF的公共部分,且AD=BF∴AD+DB=BF+DB即AB=DF如图,AB=AC,AE=AD,BD=CE,求证:△AEBADC≌△。证明:∵BD=CE∴BD-ED=CE-ED,即BE=CD。CABDE在AEB和ADC中,AB=ACAE=ADBE=CD∴△AEBADC≌△(sss)探究二:任意画一个△ABC,再画一个△A′B′C′,使AB=A′B′,BC=B′C′,CA=C′A′,判断两个三角形是否全等作法:1、画线段B′C=BC;2、分别以B′、C′为圆心,线段AB、BC为半径作弧,两弧交于点A′;3、连接线段A′B′,A′C′。结论:三边对应相等的两个三角形全等简写为:SSS我们利用前面的结论,还可以得到作一个角等于已知角的方法。例2:已知∠AOB求作:∠A′O′B′=∠AOBOABCDO′A′B′C′D′作法:1、以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;2、画一条射线O′A′,以点O′为圆心,OC长为半径画弧,交O′A′于点C′;3、以点C′为圆心,CD长为半径画弧,与第2步中所画的弧交于点D′;4、过点D′画射线O′B′,则∠A′O′B′=∠AOB小结2.三边对应相等的两个三角形全等(边边边或SSS);3.书写格式:①准备条件;②三角形全等书写的三步骤。1.知道三角形三条边的长度怎样画三角形。生活中应用