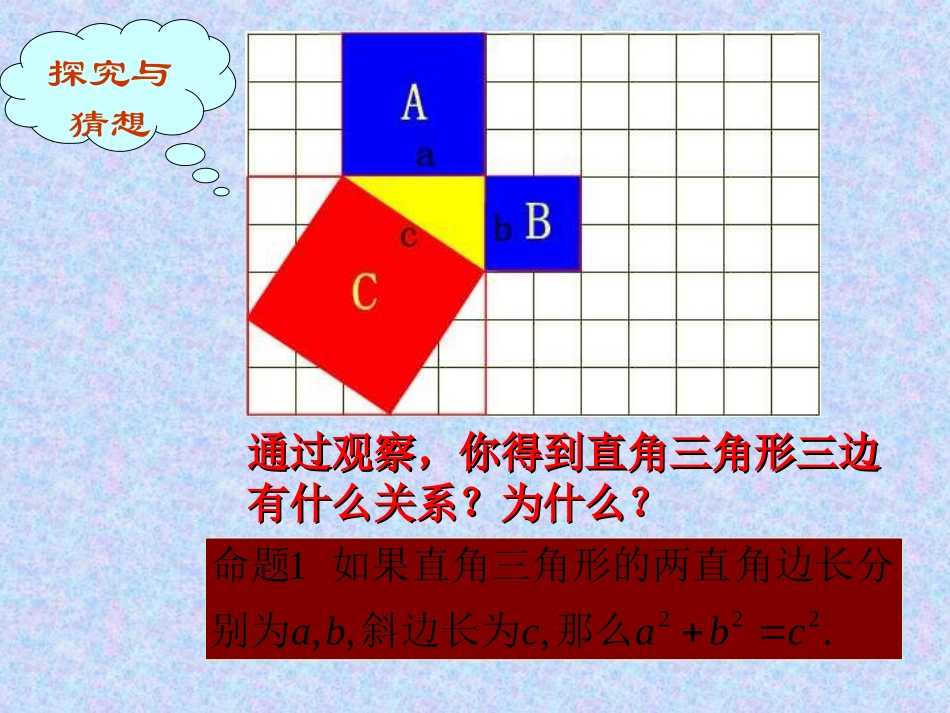
教学设计:首先猜想问题,大部分同学能考虑到关系,不能很好的总结出结论,以此激发学生的学习兴趣。引入课题。通过拼图活动,调动学生思维的积极性,由于难度比较大,组织学生开展小组合作学习。教师要巡回辅导,给予学生必要的帮助。接下来,让学生欣赏传说故事,通过故事使学生明白:科学家的伟大成就多数都是在看似平淡无奇的现象中发现和研究出来的;生活中处处有数学,我们应该学会观察、思考,将学习与生活紧密结合起来。让学生了解我国古代辉煌的数学成就。这样,一方面激发学生的求知欲望,另一方面,也对学生进行了学习方法指导和解决问题能力的培养。教师要引导学生学习科学家敏锐的观察力和勤于思考的作风,不断提高自己的数学素养,适时对大家进行思想教育。探究与猜想通过观察,你得到直角三角形三边通过观察,你得到直角三角形三边有什么关系?为什么?有什么关系?为什么?.,,,1222cbacba那么斜边长为别为角边长分如果直角三角形的两直命题利用拼图来验证勾股定理:cab1、准备四个全等的直角三角形(设直角三角形的两条直角边分别为a,b,斜边c);2、你能用这四个直角三角形拼成一个正方形吗?拼一拼试试看3、你拼的正方形中是否含有以斜边c为边的正方形?4、你能否就你拼出的图说明a2+b2=c2?cabcabcabcab=2ab+b2-2ab+a2=a2+b2∴a2+b2=c2大正方形的面积可以表示为;也可以表示为c24•+(b-a)22ab∵c2=4•+(b-a)22ab经过证明被确认正确的命题叫做经过证明被确认正确的命题叫做定理定理..cabcabcabcab∵(a+b)2=c2+4•ab/2a2+2ab+b2=c2+2ab∴a2+b2=c2大正方形的面积可以表示为;也可以表示为(a+b)2c2+4•ab/2如果直角三角形两直角边分别为a,b,斜边为c,那么a2+b2=c2即直角三角形两直角边的平方和等于斜边的平方.勾股定理cab勾股弦∵∠C=90°∴a2+b2=c2读一读勾股世界我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式。1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。利用()法,探索了直角三角形的三边关系,得到勾股定理:即直角三角形两直角边的平方和等于斜边的平方CcbaABA的面积+B的面积=C的面积a2+b2=c2面积1、下图中的三角形是直角三角形,其余是正方形,求下列图中字母所表示的正方形的面积.=625225400A22581B=144想一想ABCD7cm2.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为___________cm2。493、一高为2.5米的木梯,架在高为2米的墙上(如图),这时梯脚与墙的距离是多少米?ABC练一练练一练1、写出勾股定理。2、直角ABC的两条直角边a=3,b=4,求斜边c。5解:∵∠C=90°∴BC2+AC2=AB2又∵AC=2米AB=2.5米∴BC=AB2—AC2=1.5米1、直角ABC的两直角边a=5,b=12,c=_____2、直角ABC的一条直角边a=10,斜边c=26,则b=()。3、已知:∠C=90°,a=6,a:b=3:4,求b和c。小试牛刀小试牛刀cab13c=10b=824以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?ABCDEF议一议议一议C160904040BA例、如图所示是一个长方形零件的平面图,尺寸如图所示,求两孔中心A,B之间的距离.(单位:毫米)小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度27454762258465480∴售货员没搞错∵议一议荧屏对角线大约为74厘米4658…………再见