函数的单调性 (3)VIP免费

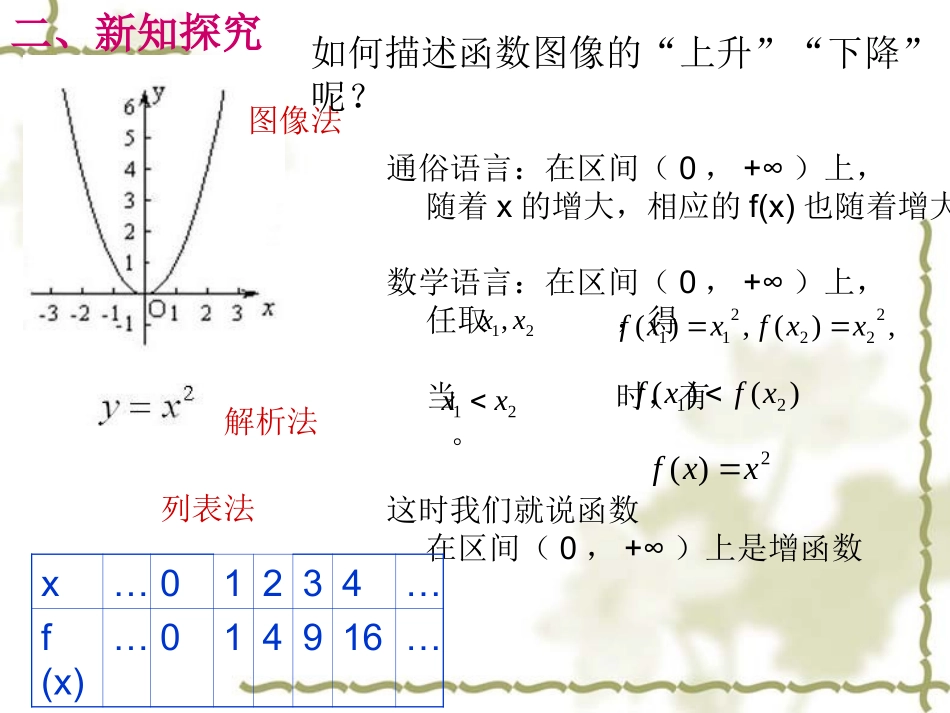
1.3.1函数的单调性函数的基本性质兰炼三中杨利军思考1：观察下列各个函数的图象，并说说它们分别反映了相应函数的哪些变化规律注意：函数的单调性是对定义域内某个区间而言的，是函数的局部性质。二、新知探究解析法图像法通俗语言：在区间（0，+∞）上，随着x的增大，相应的f(x)也随着增大。数学语言：在区间（0，+∞）上，任取，得当时，有。这时我们就说函数在区间（0，+∞）上是增函数21,xx,)(,)(222211xxfxxf21xx)()(21xfxf2)(xxfx…01234…f(x)…014916…列表法如何描述函数图像的“上升”“下降”呢？0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右，图象上升数量特征0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右，图象上升数量特征y随x的增大而增大0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右，图象上升从左至右，图象下降数量特征y随x的增大而增大0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右，图象上升从左至右，图象下降数量特征y随x的增大而增大y随x的增大而减小0yx1x2f(x2)f(x1)0yx1x2f(x2)f(x1)xx····在区间I内在区间I内图象y=f(x)y=f(x)图象特征从左至右，图象上升从左至右，图象下降数量特征y随x的增大而增大当x1＜x2时，f(x1)f(x2)那么就说在f(x)这个区间上是单调减函数，I称为f(x)的单调减区间.Oxyx1x2f(x1)f(x2)由此得出单调增函数和单调减函数的定义.xOyx1x2f(x1)f(x2)设函数y=f(x)的定义域为A,区间IA.如果对于属于定义域A内某个区间I，任取x1,x2I设函数y=f(x)的定义域为A,区间IA.如果对于属于定义域A内某个区间I上任取x1,x2I那么就说在f(x)这个区间上是单调增函数，I称为f(x)的单调区间.增当x1单调区间看下列函数图象,下列各函数有没有单调区间,若有写出其单调区间.图1图3图2没有单调区间减区间增区间,00,没有单调区间（2）函数单调性是针对某个区间而言的，是一个局部性质;有些函数在定义域内可能是单调的如y=x;有些函数在定义域内的部分区间上是增函数，而在另一部分区间上是减函数，还有的函数是非单调的，如y=c,y=2x{xN|1≤x≤5}∈（1）如果函数y=f(x)在区间D是单调增函数或单调减函数，那么就说函数y=f(x)在区间I上具有单调性。区间D叫做y=f(x)的单调区间在单调区间上，增函数的图象是上升的，减函数的图象是下降的。判断1：函数f(x)=x2在是单调增函数；,xyo2yx判断2：定义在R上的函数f(x)满足f(2)>f(1)，则函数f(x)在R上是增函数；（3）a)x1,x2取值的任意性;不能以特素质代替b)必须有大小，一般令c)同属一个单调区间yxO12f(1)f(2)12,xx12xx例1：下图是定义在区间[-5，5]上的函数y=f(x)，根据图像说出函数的单调区间以及每一单调区间上，它是增函数还是减函数？解：函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5]其中y=f(x)在区间[-5,-2),[1,3)是减函数，在区间[-2,1),[3,5]上是增函数。例2.写出单调区间1(1)(0);yxxx1yxy1yx的单调减区间是_____________(,0)(0,),讨论1：1(0)(,0)(0,)yxx能不能说在定义域上是单调减函数?？不能——数形结合的思想要了解某函数在某一区间上是否具有单调性，从图象上进行观察是一种常用的方法，但这种方法比较粗略。严格地说，它还需要进行证明。（4）若函数f(x)在其定义域内的两个区间A,B上都是增(或减）函数一般不能简单认为f(x)在AB∪上是增（减）函数yoxoyxyox在(-∞,+∞)是减函数在(-∞,0)和(0,+∞)是减函数在...