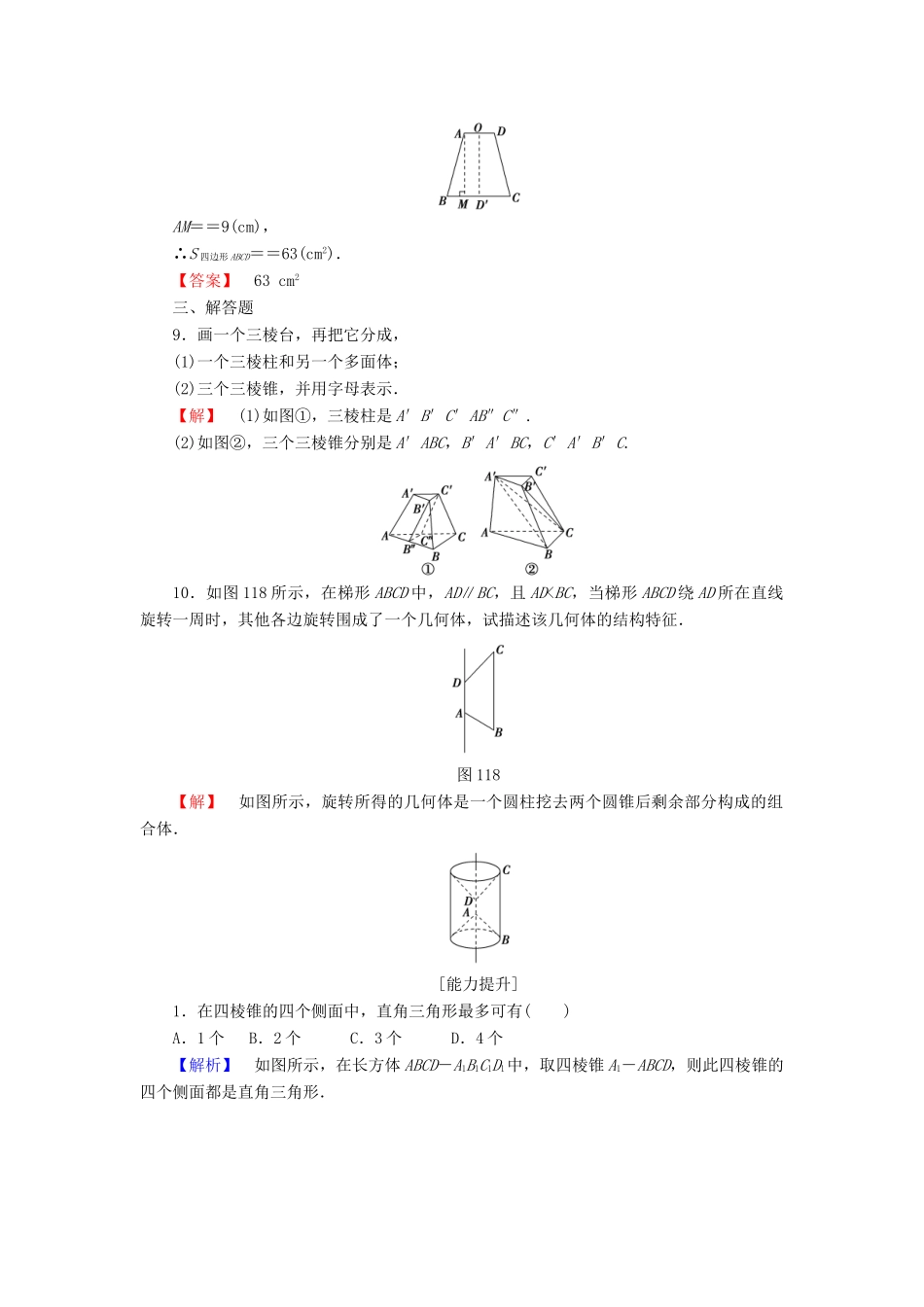
【课堂新坐标】2016-2017学年高中数学第一章立体几何初步学业分层测评1简单几何体北师大版必修2(建议用时:45分钟)[学业达标]一、选择题1.如图115是由哪个平面图形旋转得到的()图115【解析】图中给出的组合体是一个圆台上接一个圆锥,因此平面图形应由一个直角三角形和一个直角梯形构成,并且上面应是直角三角形,下面应是直角梯形.【答案】A2.一个多边形沿垂直于它所在平面的方向平移一段距离可以形成的几何体是()A.棱锥B.棱柱C.平面D.长方体【解析】平移后形成的几何体是以此多边形(起点处和终点处)为两底面的棱柱,故选B.【答案】B3.如图116,E,F,G,H是三棱柱对应边上的中点,过此四点作截面EFGH,则截面以下的几何体是()图116A.棱柱B.棱台C.棱锥D.五面体【解析】选择左右两个平行平面为底面,则它符合棱柱的结构特征,故选A.【答案】A4.下列结论正确的是()【导学号:10690002】A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线【解析】A是错误的,例如由两个相同的三棱锥叠放在一起构成的几何体,各个面都是三角形,但它不是棱锥;B是错误的,直角三角形绕着直角边旋转一周形成的面所围成的几何体才是圆锥;C是错误的,若六棱锥的所有棱长都相等,则底面多边形是正六边形,由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长,故选D.【答案】D5.如图117所示的几何体是由一个圆柱挖去一个以圆柱上底面为底面,下底面圆心为顶点的圆锥而得到的组合体,现用一个竖直的平面去截这个组合体,则截面图形可能是()甲乙图117A.①②B.①③C.①④D.①⑤【解析】一个圆柱挖去一个圆锥后,剩下的几何体被一个竖直的平面所截后,圆柱的轮廓是矩形除去一条边,圆锥的轮廓是三角形除去一条边或抛物线的一部分.【答案】D二、填空题6.直角三角形围绕其斜边所在的直线旋转得到的旋转体由________组成.【解析】所得旋转体如图,是由两个圆锥组成的.【答案】两个圆锥7.下列命题中错误的是________.①过球心的截面所截得的圆面的半径等于球的半径;②母线长相等的不同圆锥的轴截面的面积相等;③圆台所有平行于底面的截面都是圆;④圆锥所有的轴截面都是全等的等腰三角形.【解析】因为圆锥的母线长一定,根据三角形面积公式,当两条母线的夹角为90°时,过圆锥顶点的截面面积最大.【答案】②8.圆台两底面半径分别是2cm和5cm,母线长是3cm,则它的轴截面的面积是________.【解析】画出轴截面,如图,过A作AM⊥BC于M,则BM=5-2=3(cm),AM==9(cm),∴S四边形ABCD==63(cm2).【答案】63cm2三、解答题9.画一个三棱台,再把它分成,(1)一个三棱柱和另一个多面体;(2)三个三棱锥,并用字母表示.【解】(1)如图①,三棱柱是A′B′C′AB″C″.(2)如图②,三个三棱锥分别是A′ABC,B′A′BC,C′A′B′C.10.如图118所示,在梯形ABCD中,AD∥BC,且AD