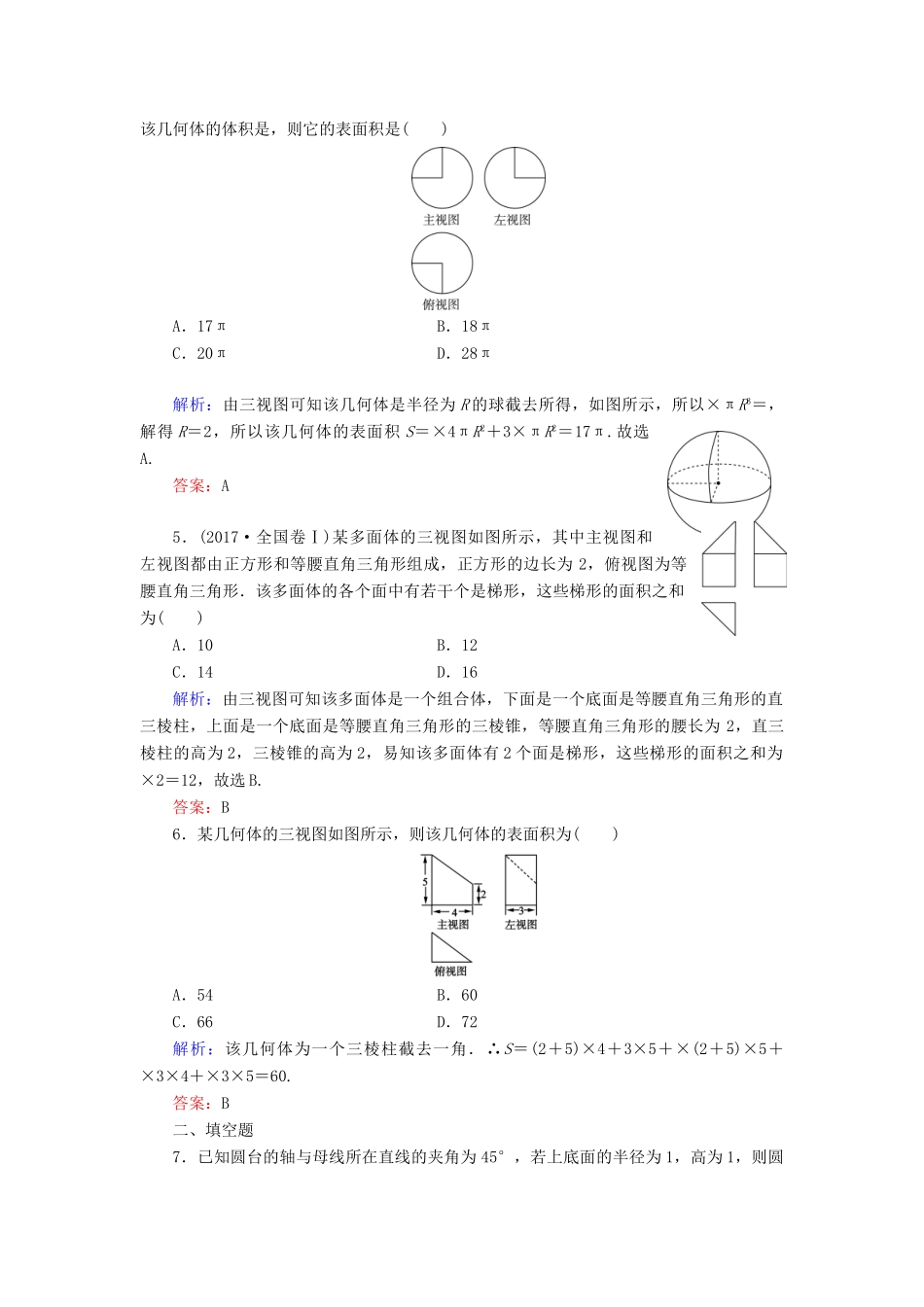
7.1柱、锥、台的侧面展开与面积课时跟踪检测一、选择题1.已知某几何体的三视图如下图所示,则该几何体的表面积是()A.5+2B.6+C.6+2D.5+解析:此几何体为三棱柱,其表面积为×1×1×2+2×1+2×1+×2=5+2.答案:A2.一个棱锥的三视图如图(单位:cm),则该棱锥的表面积为()A.24B.48C.48+6D.48+12解析:依题意得,该几何体是一个底面为等腰直角三角形(直角边长为6)、高为4的三棱锥,其表面积等于×6×6+×6×5×2+×6×=48+12.答案:D3.一个几何体的三视图如图所示,其主视图和左视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是()A.6πB.12πC.18πD.24π解析:结合三视图可知该几何体是一个圆台,其上,下底面的半径分别为2,1,则该几何体的侧面积S=π(2×4+1×4)=12π.答案:B4.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π解析:由三视图可知该几何体是半径为R的球截去所得,如图所示,所以×πR3=,解得R=2,所以该几何体的表面积S=×4πR2+3×πR2=17π.故选A.答案:A5.(2017·全国卷Ⅰ)某多面体的三视图如图所示,其中主视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A.10B.12C.14D.16解析:由三视图可知该多面体是一个组合体,下面是一个底面是等腰直角三角形的直三棱柱,上面是一个底面是等腰直角三角形的三棱锥,等腰直角三角形的腰长为2,直三棱柱的高为2,三棱锥的高为2,易知该多面体有2个面是梯形,这些梯形的面积之和为×2=12,故选B.答案:B6.某几何体的三视图如图所示,则该几何体的表面积为()A.54B.60C.66D.72解析:该几何体为一个三棱柱截去一角.∴S=(2+5)×4+3×5+×(2+5)×5+×3×4+×3×5=60.答案:B二、填空题7.已知圆台的轴与母线所在直线的夹角为45°,若上底面的半径为1,高为1,则圆台的下底面半径为________.解析:轴截面如图,r′=1,r=1+AB=1+|A1A|=1+1=2.答案:28.已知正四棱锥的底面边长为4cm,高与斜高的夹角为30°,则该正四棱锥的侧面积等于________cm2.解析:如图,正四棱锥的高PO、斜高PE、底面边心距OE组成Rt△POE.因为OE=×4=2(cm),∠OPE=30°,所以PE==4(cm).所以S侧面积=×4×4×4=32(cm2).答案:329.已知某几何体的三视图如图所示,则该几何体的表面积等于________.解析:如图,该几何体为三棱柱ABC-A1B1C1截去一个三棱锥D-A1B1C1得到,如图,∴表面积为:×4×4+×(4+8)×4+×(4+8)×4+4×8+×4×4=8+24+24+32+8=64+32.答案:64+32三、解答题10.圆台的上、下底面半径分别是10cm和20cm,它的侧面展开图的扇环的圆心角是180°,那么圆台的表面积是多少?解:上底面周长为2π×10=20π(cm),下底面周长为2π×20=40π(cm),∴展开图中内弧长为:π·SA=20π,则SA=20,外弧长为:π·SB=40π,则SB=40,∴AB=40-20=20,即母线长l=20(cm).∴S表=S侧+S上+S下=π(10+20)×20+π×102+π×202=1100π(cm2).所以圆台的表面积为1100πcm2.11.已知四棱锥S-ABCD的底面是菱形,AC=80cm,BD=60cm,AC∩BD=O,SO⊥平面ABCD,SO=32cm.求它的侧面积.解:如图,AC=80cm,BD=60cm.则AO=40cm,OB=30cm,由于AC⊥BD,∴AB==50(cm).过O向BC作垂线,垂足为M,连接SM.由OM·BC=OB·OC,知OM===24(cm).∴SM===40(cm),∴S侧=4××BC×SM=4××50×40=4000(cm2).12.如图所示是一建筑物的三视图,现需将其外壁用油漆刷一遍,已知每平方米用漆0.2kg,问需要多少油漆?(尺寸如图,单位:m,π取3.14,结果精确到0.01kg)解:由三视图知建筑物为一组合体,上部为一圆锥,下部为一四棱柱.圆锥底面半径为3m,母线长为5m,四棱柱高为4m,底面是边长为3m的正方形.圆锥的表面积为:πr2+πrl=3.14×32+3.14×3×5=28.26+47.1=75.36.四棱柱的一个底面积为32=9.四棱柱的侧面积为:4×4×3=4...