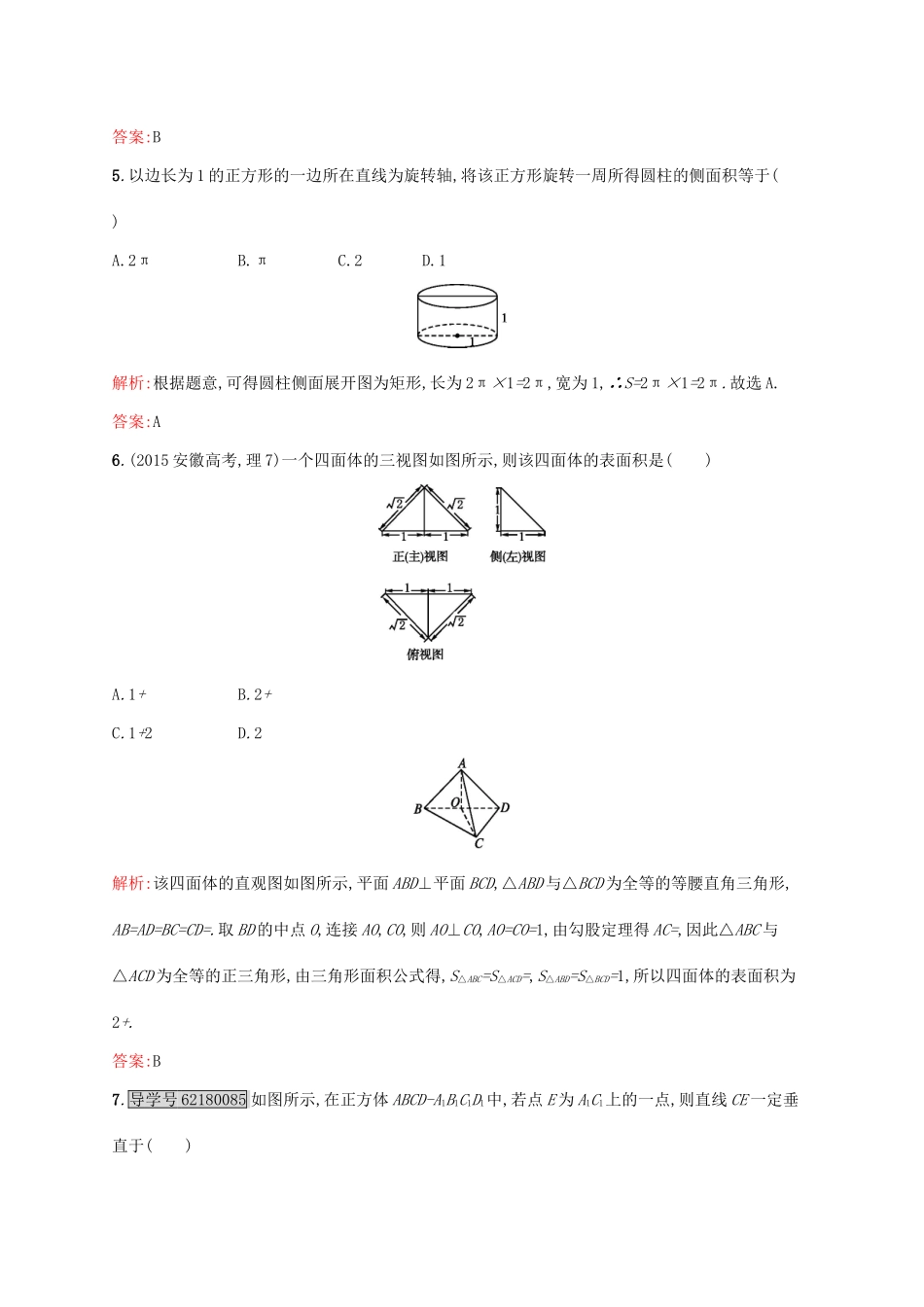
第一章测评(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图所示,观察四个几何体,其中判断正确的是()A.①是棱台B.②是圆台C.③是棱锥D.④不是棱柱答案:C2.如图所示,△O'A'B'是水平放置的△OAB的直观图,则△OAB的面积是()A.6B.3C.6D.12解析:△OAB是直角三角形,其两条直角边的长分别是4和6,则其面积是12.答案:D3.若三个球的半径之比是1∶2∶3,则半径最大的球的体积是其余两球的体积和的()A.4倍B.3倍C.2倍D.1倍解析:设三个球的半径依次为a,2a,3a,V最大=π(3a)3=36πa3,V1+V2=πa3+π(2a)3=πa3=12πa3,=3.答案:B4.若一个圆台的上、下底面半径和高的比为1∶4∶4,圆台的侧面积为400π,则该圆台的母线长为()A.10B.20C.12D.24解析:设圆台上底面半径为r,则下底面半径、高分别为4r,4r,于是其母线l==5r,又侧面积为400π,所以π(r+4r)·5r=400π,解得r=4,于是母线长为20.答案:B5.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于()A.2πB.πC.2D.1解析:根据题意,可得圆柱侧面展开图为矩形,长为2π×1=2π,宽为1,∴S=2π×1=2π.故选A.答案:A6.(2015安徽高考,理7)一个四面体的三视图如图所示,则该四面体的表面积是()A.1+B.2+C.1+2D.2解析:该四面体的直观图如图所示,平面ABD⊥平面BCD,△ABD与△BCD为全等的等腰直角三角形,AB=AD=BC=CD=.取BD的中点O,连接AO,CO,则AO⊥CO,AO=CO=1,由勾股定理得AC=,因此△ABC与△ACD为全等的正三角形,由三角形面积公式得,S△ABC=S△ACD=,S△ABD=S△BCD=1,所以四面体的表面积为2+.答案:B7.导学号62180085如图所示,在正方体ABCD-A1B1C1D1中,若点E为A1C1上的一点,则直线CE一定垂直于()A.ACB.BDC.A1DD.A1D1解析:连接AC,由于BD⊥AC,BD⊥AA1,AC∩AA1=A,所以BD⊥平面ACC1A1.又因为CE⫋平面ACC1A1,所以CE⊥BD.答案:B8.已知平面α⊥平面β,α∩β=l,则下列命题错误的是()A.如果直线a⫋α,那么直线a必垂直于平面β内的无数条直线B.如果直线a⫋α,那么直线a不可能与平面β平行C.如果直线a⫋α,a⊥l,那么直线a⊥平面βD.平面α内一定存在无数条直线垂直于平面β内的所有直线解析:A选项中直线a必定与平面β内无数条平行直线垂直,故正确;B选项中如果a⫋α,a∥l,则a∥β,故错误;由面面垂直的性质定理可知C选项正确;在平面α内,垂直于交线l的直线,都垂直于平面β,也就垂直于平面β内的所有直线,故D选项正确.答案:B9.正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为()A.B.16πC.9πD.解析:由图知,R2=(4-R)2+2,∴R2=16-8R+R2+2,∴R=,∴S表=4πR2=4π×π,选A.答案:A10.设α,β是两个不同的平面,l是一条直线,给出下列说法:①若l⊥α,α⊥β,则l⫋β②若l∥α,α∥β,则l⫋β③若l⊥α,α∥β,则l⊥β④若l∥α,α⊥β,则l⊥β其中说法正确的个数为()A.1B.2C.3D.0解析:对于①,若l⊥α,α⊥β,则l∥β或l⫋β,故①错误;对于②,若l∥α,α∥β,则l⫋β或l∥β,故②错误;对于③,若l⊥α,α∥β,则l⊥β,故③正确;对于④,若l∥α,α⊥β,则l⫋β或l∥β或l⊥β或l与β斜交,故④错误.答案:A11.一块石材表示的几何体的三视图如图所示.将该石材切削、打磨,加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4解析:由三视图可得原石材为如图所示的直三棱柱A1B1C1-ABC,且AB=8,BC=6,BB1=12.若要得到半径最大的球,则此球与平面A1B1BA,BCC1B1,ACC1A1相切,故此时球的半径与△ABC内切圆的半径相等,故半径r==2.故选B.答案:B12.如图所示,在棱长均相等的三棱锥P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论不成立的是()A.BC∥平面PDFB.DF⊥平面PAEC.平面PDF⊥平面PAED.平面PDE⊥平面ABC解析:由BC∥DF,易得BC∥平面PDF,A成立;易证BC⊥平面PAE,BC∥DF,所以结论B,C均成立;点P在底面ABC上的射影为△ABC的中心,不在中位线DE上,故结论D不成立.答案:D二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)13.一水平放置的平面图形OABC,用斜二测画法画出它的直观图O'A'B'C'如图所示,此直观图恰好是一个边长为2的正方形,则原平面图形OABC的面积为.解...