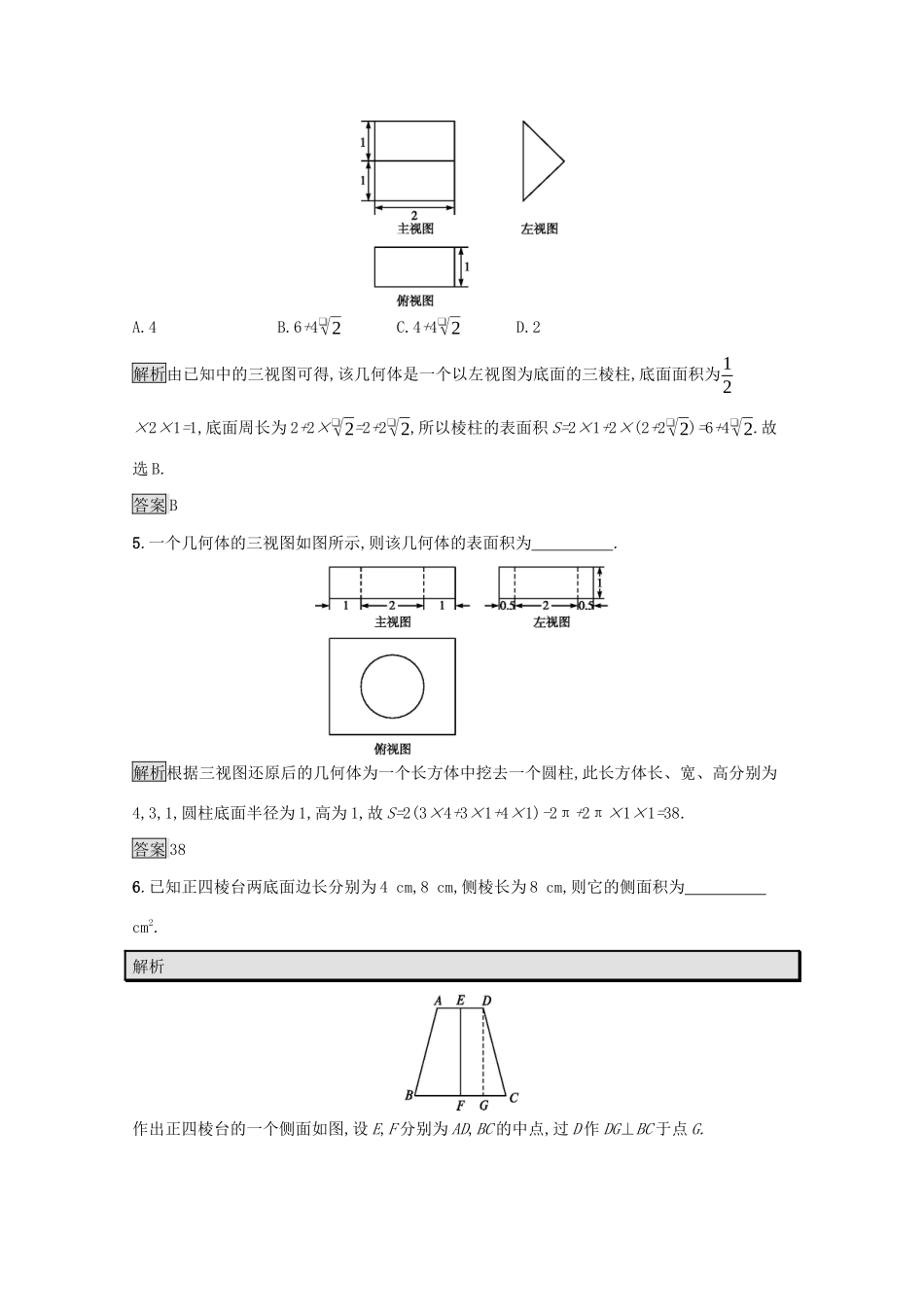
7.1柱、锥、台的侧面展开与面积课后篇巩固探究1.若圆锥的底面直径为6,高是4,则它的侧面积为()A.12πB.24πC.15πD.30π解析由已知得圆锥的母线长为❑√32+42=5,于是侧面积S=π×3×5=15π.答案C2.(2018全国Ⅰ卷,文5)已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A.12❑√2πB.12πC.8❑√2πD.10π解析过直线O1O2的平面截该圆柱所得的截面为圆柱的轴截面,设底面半径为r,母线长为l,因为轴截面是面积为8的正方形,所以2r=l=2❑√2,r=❑√2,所以圆柱的表面积为2πrl+2πr2=8π+4π=12π.答案B3.若圆台的高为3,一个底面半径是另一个底面半径的2倍,其轴截面的一个底角为45°,则这个圆台的侧面积是()A.27πB.27❑√2πC.9❑√2πD.36❑√2π解析设圆台上底半径为r1,下底半径为r2,母线长为l,如图所示,2r2=2r1+6=4r1,∴r1=3,r2=6.S圆台侧=π(r1+r2)l=π(6+3)×3❑√2=27❑√2π.答案B4.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为()A.4B.6+4❑√2C.4+4❑√2D.2解析由已知中的三视图可得,该几何体是一个以左视图为底面的三棱柱,底面面积为12×2×1=1,底面周长为2+2×❑√2=2+2❑√2,所以棱柱的表面积S=2×1+2×(2+2❑√2)=6+4❑√2.故选B.答案B5.一个几何体的三视图如图所示,则该几何体的表面积为.解析根据三视图还原后的几何体为一个长方体中挖去一个圆柱,此长方体长、宽、高分别为4,3,1,圆柱底面半径为1,高为1,故S=2(3×4+3×1+4×1)-2π+2π×1×1=38.答案386.已知正四棱台两底面边长分别为4cm,8cm,侧棱长为8cm,则它的侧面积为cm2.解析作出正四棱台的一个侧面如图,设E,F分别为AD,BC的中点,过D作DG⊥BC于点G.由题知AD=4cm,BC=8cm,CD=8cm,得DE=2cm,FC=4cm,解得GC=2cm,在Rt△DGC中,DG=❑√82-22=2❑√15(cm),即斜高为2❑√15cm,所以所求侧面积为12×(16+32)×2❑√15=48❑√15(cm2).答案48❑√157.已知正四棱锥底面正方形的边长为4cm,高与斜高夹角为30°,其侧面积为cm2,全面积为cm2.解析如图所示,正四棱锥的高PO,斜高PE,底面边心距OE组成Rt△POE.∵OE=2cm,∠OPE=30°,∴斜高h'=PE=OEsin30°=212=4(cm).∴S正四棱锥侧=12ch'=12×4×4×4=32(cm2),S正四棱锥全=42+32=48(cm2).答案32488.在底面是菱形的直四棱柱中,它的对角线长分别为9和15,高是5,求该直四棱柱的侧面积.解如图所示,设底面对角线AC=a,BD=b,交点为O,对角线A1C=15,BD1=9.故有a2+52=152,b2+52=92,所以a2=200,b2=56.因为底面是菱形,所以AB2=(AC2)2+(BD2)2=a2+b24=200+564=64,即AB=8.所以该直四棱柱的侧面积S=4×8×5=160.9.圆锥的高和底面半径相等,它的一个内接圆柱的高和圆柱底面半径也相等,求圆柱的表面积和圆锥的表面积之比.解如图所示,设圆柱和圆锥的底面半径分别为r,R,圆锥母线长为l,则rR=R-rR,即rR=12.∴R=2r,l=❑√2R.∴S圆柱表S圆锥表=2πr2+2πr2πR·❑√2R+πR2=4πr24❑√2πr2+4πr2=1❑√2+1=❑√2-1.10.导学号91134026如图所示,在三棱锥S-ABC中,SA⊥平面ABC,△ABC是直角三角形,∠ACB=90°,∠ABC=30°,AC=1,SB=2❑√3.求三棱锥S-ABC的表面积.解∵SA⊥平面ABC,∴SA⊥BC.∵∠ACB=90°,∴AC⊥BC.又SA∩AC=A,∴BC⊥平面SAC,∴SC⊥BC.∴四个面都是直角三角形.∵∠ABC=30°,AC=1,∴在Rt△ABC中,AB=2,BC=❑√3,在Rt△SCB中,SC=❑√SB2-BC2=3,在Rt△SAB中,SA=❑√SB2-AB2=2❑√2.∴S△SBC=12SC·BC=3❑√32,S△ABC=12AC·BC=❑√32,S△SAB=12SA·AB=2❑√2,S△SAC=12SA·AC=❑√2.∴三棱锥的表面积S表=S△ABC+S△SBC+S△SAB+S△SAC=2❑√3+3❑√2.