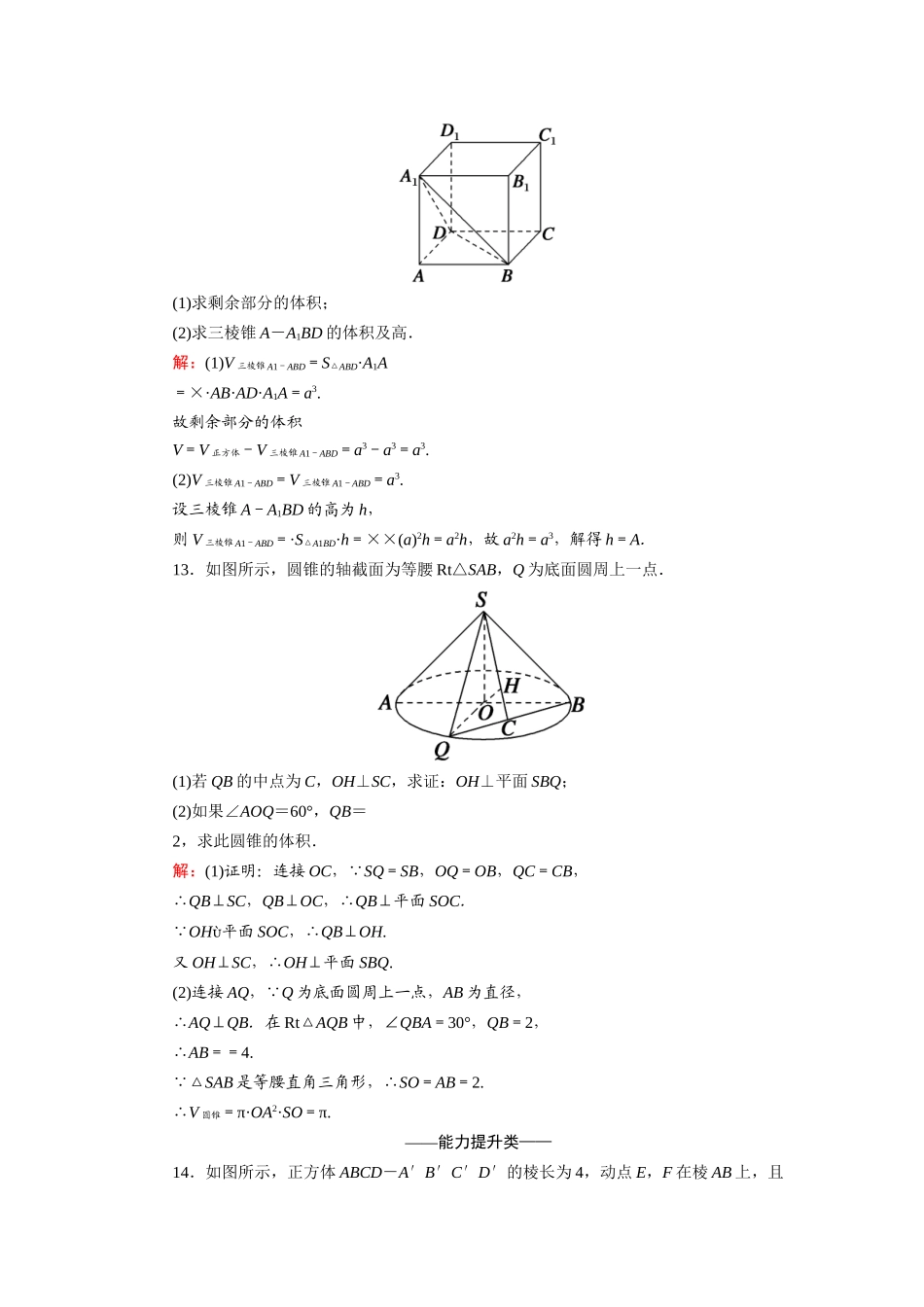
课时作业11柱体与锥体的体积时间:45分钟——基础巩固类——一、选择题1.将两个棱长为10cm的正方体铜块熔化后铸成底面边长为5cm的正四棱柱,则该四棱柱的高为(B)A.8cmB.80cmC.40cmD.cm解析:设正四棱柱的高为hcm,依题意得5×5×h=2×103,解得h=80(cm).2.若一个圆锥的轴截面(过圆锥顶点和底面直径的截面)是等边三角形,其面积为,则这个圆锥的体积为(B)A.3πB.πC.πD.π解析:设圆锥的底面半径为R,依题意知该圆锥的高即轴截面的高h=·2R=R,所以·2R·R=,解得R=1.所以V=×π×12×=π.3.正三棱柱的侧面展开图是边长为2和4的矩形,则该正三棱柱的体积是(D)A.B.C.D.或解析:当2为正三棱柱的底面周长时,正三棱柱底面三角形的边长a=,底面面积S=a2=,正三棱柱的高h=4,所以正三棱柱的体积V=Sh=;当4为正三棱柱的底面周长时,正三棱柱底面三角形的边长a′=,底面面积S′=a′2=,正三棱柱的高h′=2,所以正三棱柱的体积V′=S′h′=.所以正三棱柱的体积为或.4.半径为R的半圆卷成一个圆锥,则它的体积是(A)A.πR3B.πR3C.πR3D.πR3解析:令母线长为l,底面半径为r,则πl=2πr,∴l=2r. l=R,∴r=R.高h===R.∴V=πr2h=π·R2·R=πR3.5.已知直角三角形两直角边长分别为a、b,分别以这两个直角边为轴,旋转所形成的几何体的体积比为(B)A.abB.baC.a3b3D.b3a3解析:以a为轴的几何体的体积为,以b为轴的几何体的体积为,∴体积比为bA.6.设正棱锥的高和底面边长都缩小为原来的,则它的体积是原来的(B)A.B.C.D.解析: V=·S·h,h′=h,S′=S,∴=.7.在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体体积为(D)A.B.C.D.解析:每个截去的小三棱锥体积为×(××)×=×()4,则剩余部分的体积为V=1-×()4×8=1-=.8.《算数书》竹简于20世纪80年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3,那么,近似公式V≈L2h相当于将圆锥体积公式中的π近似取为(B)A.B.C.D.解析:V=πr2h≈L2h,而L=2πr,则π=.二、填空题9.一个长方体的三个面的面积分别是,,,则这个长方体的体积为.解析:设长方体的棱长分别为a,b,c,则三式相乘可知(abc)2=6,所以长方体的体积V=abc=.10.若圆锥的侧面积为2π,底面面积为π,则该圆锥的体积为π.解析:本题考查圆锥的侧面积、体积以及圆锥中基本量的关系、运算,只需求出基本量代入公式即可.设圆锥底面半径为r,母线长为l,则,∴,∴圆锥的高h==,∴V=Sh=×π×=π.11.将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积为a3.解析: BA=BC=BD,∴B点在面ACD上的射影为△ACD的外心,即等腰Rt△ADC斜边中点O,OD=a,∴OB=a,∴V=a2·a×=a3.三、解答题12.如图所示,正方体ABCD-A1B1C1D1的棱长为a,过顶点B,D,A1截下一个三棱锥.(1)求剩余部分的体积;(2)求三棱锥A-A1BD的体积及高.解:(1)V三棱锥A1-ABD=S△ABD·A1A=×·AB·AD·A1A=a3.故剩余部分的体积V=V正方体-V三棱锥A1-ABD=a3-a3=a3.(2)V三棱锥A1-ABD=V三棱锥A1-ABD=a3.设三棱锥A-A1BD的高为h,则V三棱锥A1-ABD=·S△A1BD·h=××(a)2h=a2h,故a2h=a3,解得h=A.13.如图所示,圆锥的轴截面为等腰Rt△SAB,Q为底面圆周上一点.(1)若QB的中点为C,OH⊥SC,求证:OH⊥平面SBQ;(2)如果∠AOQ=60°,QB=2,求此圆锥的体积.解:(1)证明:连接OC, SQ=SB,OQ=OB,QC=CB,∴QB⊥SC,QB⊥OC,∴QB⊥平面SOC. OH平面SOC,∴QB⊥OH.又OH⊥SC,∴OH⊥平面SBQ.(2)连接AQ, Q为底面圆周上一点,AB为直径,∴AQ⊥QB.在Rt△AQB中,∠QBA=30°,QB=2,∴AB==4. △SAB是等腰直角三角形,∴SO=AB=2.∴V圆锥=π·OA2·SO=π.——能力提升类——14.如图所示,正...