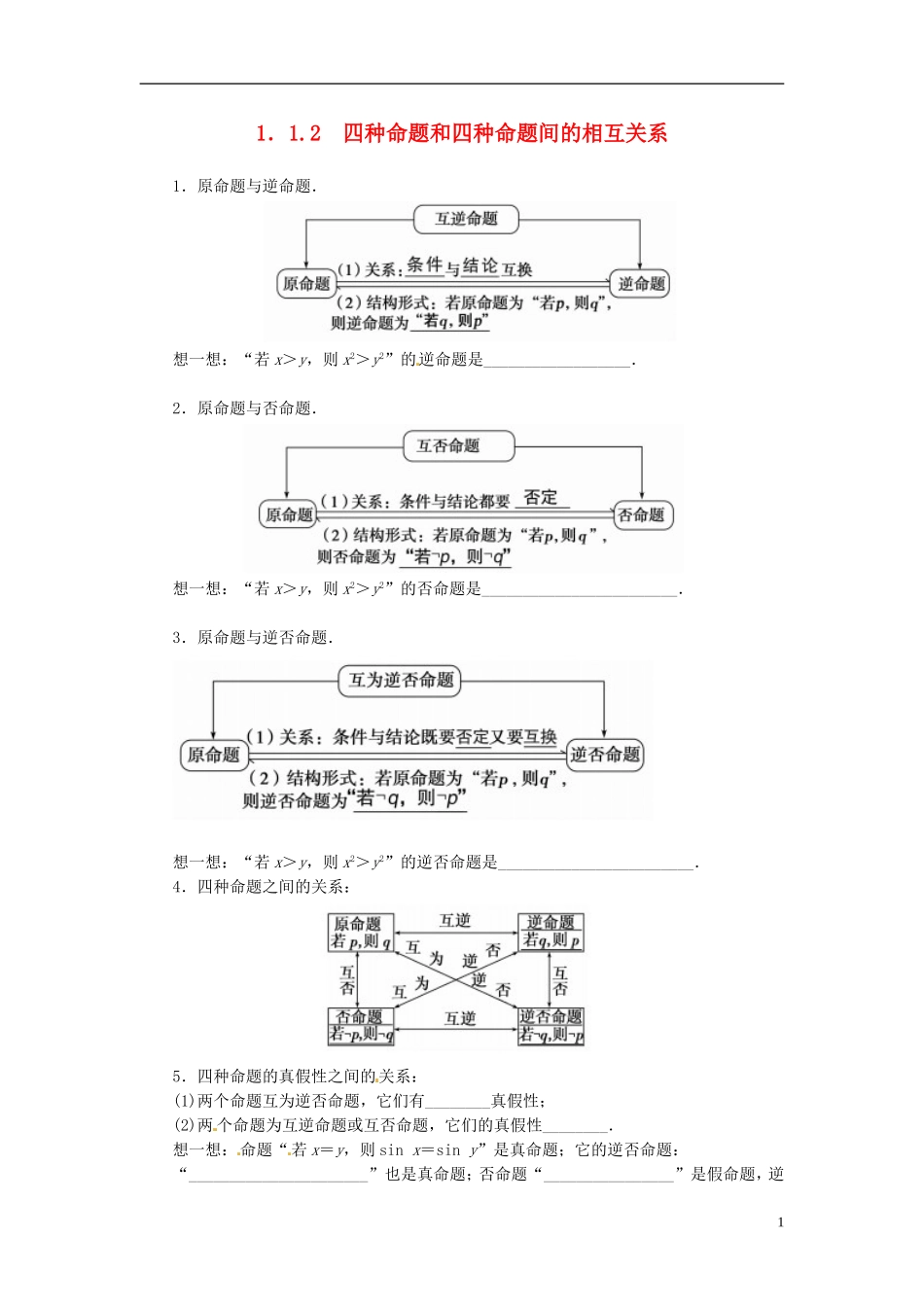
1.1.2四种命题和四种命题间的相互关系1.原命题与逆命题.想一想:“若x>y,则x2>y2”的逆命题是__________________.2.原命题与否命题.想一想:“若x>y,则x2>y2”的否命题是________________________.3.原命题与逆否命题.想一想:“若x>y,则x2>y2”的逆否命题是________________________.4.四种命题之间的关系:5.四种命题的真假性之间的关系:(1)两个命题互为逆否命题,它们有________真假性;(2)两个命题为互逆命题或互否命题,它们的真假性________.想一想:命题“若x=y,则sinx=siny”是真命题;它的逆否命题:“______________________”也是真命题;否命题“________________”是假命题,逆1命题“________________________________________________________________________”也是假命题.基础梳理1.(1)条件结论(2)“若q,则p”想一想:若x2>y2,则x>y2.(1)否定(2)“若綈p,则綈q”想一想:若x≤y,则x2≤y23.(1)否定互换(2)“若綈q,则綈p”想一想:若x2≤y2,则x≤y5.相同的没有关系想一想:若sinx≠siny,则x≠y若x≠y,则sinx≠siny若sinx=siny,则x=y1.命题“若a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为()A.1个B.2个C.3个D.4个2.命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是()A.若f(x)是偶函数,则f(-x)是偶函数B.若f(x)不是奇函数,则f(-x)不是奇函数C.若f(-x)是奇函数,则f(x)是奇函数D.若f(-x)不是奇函数,则f(x)不是奇函数3.有下列四个命题:(1)“若x+y=0,则x,y互为相反数”的否命题;(2)“若x>y,则x20”的否命题;(4)“等边三角形有两边相等”的逆命题.其中真命题的个数是()A.0个B.1个C.2个D.3个自测自评1.解析:由a>-3⇒a>-6,但由a>-6D⇒/a>-3,故真命题是原命题及原命题的逆否命题,故选B.答案:B2.B3.解析:(1)是真命题.其逆命题为“若x,y互为相反数,则x+y=0”,是真命题,因为原命题的否命题与其逆命题有相同的真假性,所以其否命题是真命题.(2)是假命题.原命题(如取x=1,y=0)是假命题,所以其逆否命题是假命题.(3)是假命题.该命题否命题为“若x>3,则x2-x-6≤0”,显然是假命题.(4)是假命题.该命题的逆命题是“有两边相等的三角形是等边三角形”,显然是假命题.答案:B21.下列命题中,正确的个数是()①“若x,y都是奇数,则x+y是偶数”的否命题;②“全等三角形是相似三角形”的逆命题;③“圆内接四边形对角互补”的逆否命题.A.3个B.2个C.1个D.0个1.C2.命题“若A∩B=A,则A⊆B”的逆否命题是()A.若A∪B≠A,则A⊇BB.若A∩B≠A,则A⃘BC.若A⃘B,则A∩B≠AD.若A⊇B,则A∩B≠A2.解析:先明确条件和结论,再根据要求进行转换.答案:C3.(2014·杭州高二检测)命题“如果x≥a2+b2,那么x≥2ab”的等价命题是()A.如果x<a2+b2,那么x<2abB.如果x≥2ab,那么x≥a2+b2C.如果x<2ab,那么x<a2+b2D.如果x≥a2+b2,那么x<2ab3.解析:等价命题即为原命题的逆否命题,故选C.答案:C4.命题“若α=β,则sinα=sinβ”的等价命题是____________________.4.解析:原命题与逆否命题是等价命题,所以,命题“若α=β,则sinα=sinβ”的等价命题是“若sinα≠sinβ,则α≠β”.答案:若sinα≠sinβ,则α≠β5.命题“若函数f(x)=logax(a>0,a≠1)在其定义域内是减函数,则loga2<0”的逆否命题是()A.若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数B.若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数C.若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数D.若loga2<0,则函数f(x)=logax(a>0,a≠1)在其定义域内是减函数5.解析:由互为逆否命题的关系可知,原命题的逆否命题为:若loga2≥0,则函数f(x)=logax(a>0,a≠1)在其定义域内不是减函数.答案:A6.设原命题:若a+b≥2,则a,b中至少有一个不小于1,则原命题与其逆命题的真假情况是()A.原命题真,逆命题假B.原命题假,逆命题真C.原命题...