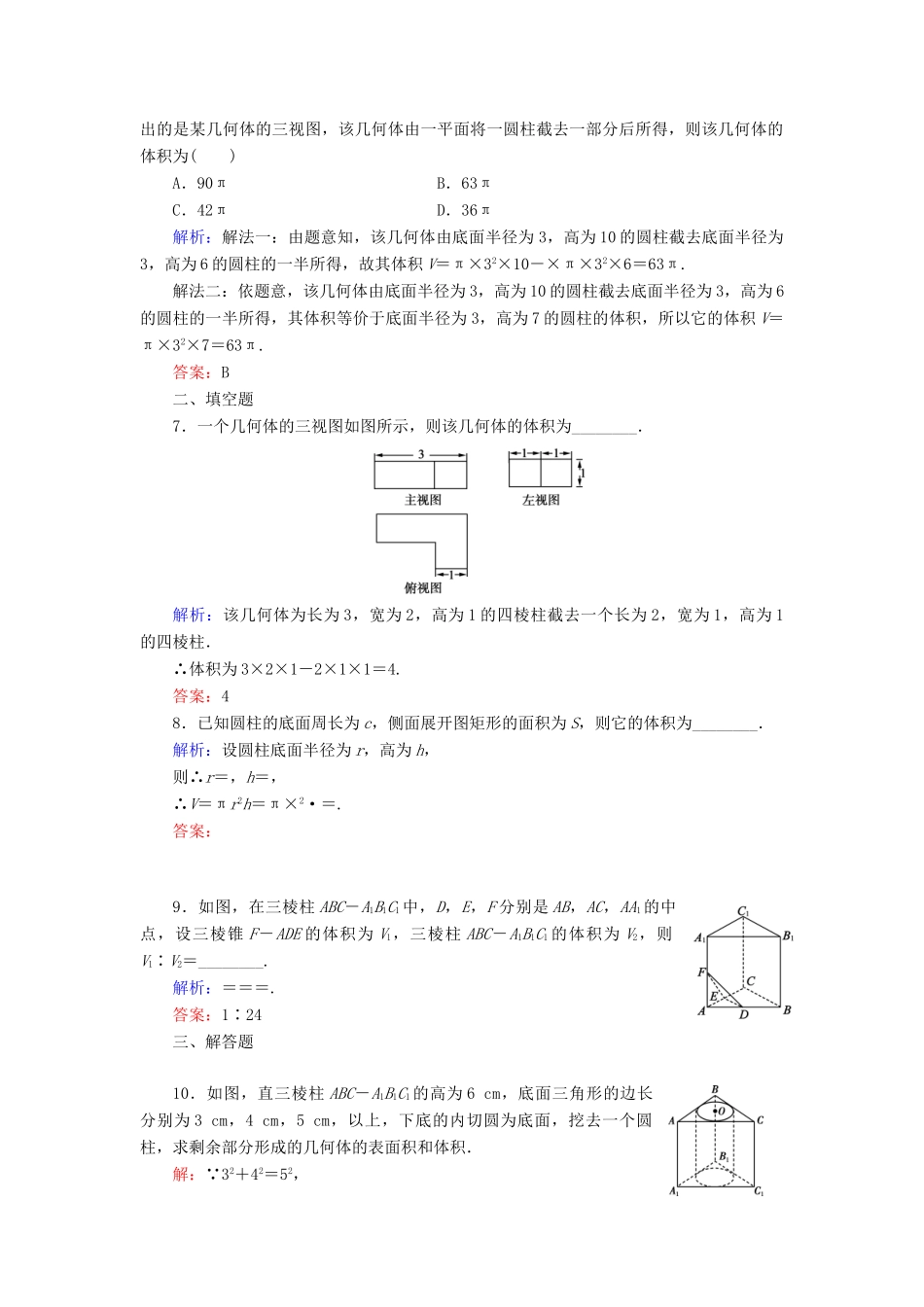
7.2柱、锥、台的体积课时跟踪检测一、选择题1.(2018·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.2B.4C.6D.8解析:根据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上下底分别为1,2,梯形的高为2,因此几何体的体积为×(1+2)×2×2=6,故选C.答案:C2.一个几何体的三视图如图所示,则这个几何体的体积等于()A.12B.4C.D.解析:如图,此几何体为四棱锥.V=××2=4.答案:B3.如下图,某几何体的主视图与左视图都是边长为1的正方形,且体积为.则该几何体的俯视图可以是()解析:当俯视图为C时,有体积V=×1×1×1=,其它体积均不为.答案:C4.一个几何体的三视图如图所示,则该几何体的体积是()A.π+4B.2π+4C.π+4D.π+2解析:该几何体为半个圆柱与长方体的组合体V=×π×12×2+1×2×2=π+4.答案:C5.在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上的一点,它的主视图和左视图如图所示,则下列命题正确的是()A.AD⊥平面PBC,且三棱锥D-ABC的体积为B.BD⊥平面PAC,且三棱锥D-ABC的体积为C.AD⊥平面PBC,且三棱锥D-ABC的体积为D.BD⊥平面PAC,且三棱锥D-ABC的体积为解析:由正视图可得PA=AC=4,点D为棱PC的中点,由侧视图得BC=4.因为PA⊥平面ABC,BC平面ABC,所以PA⊥BC.又BC⊥AC,PA∩AC=A,所以BC⊥平面PAC,故BD与平面PAC不垂直,排除B、D;AD平面PAC,所以AD⊥BC.又在等腰直角三角形PAC中,点D是斜边PC的中点,所以AD⊥PC,又BC∩PC=C,所以AD⊥平面PBC.且三棱锥D-ABC的体积VD-ABC=VB-ACD=××4×2×4=,C正确,A错误,故选C.答案:C6.(2017·全国卷Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A.90πB.63πC.42πD.36π解析:解法一:由题意知,该几何体由底面半径为3,高为10的圆柱截去底面半径为3,高为6的圆柱的一半所得,故其体积V=π×32×10-×π×32×6=63π.解法二:依题意,该几何体由底面半径为3,高为10的圆柱截去底面半径为3,高为6的圆柱的一半所得,其体积等价于底面半径为3,高为7的圆柱的体积,所以它的体积V=π×32×7=63π.答案:B二、填空题7.一个几何体的三视图如图所示,则该几何体的体积为________.解析:该几何体为长为3,宽为2,高为1的四棱柱截去一个长为2,宽为1,高为1的四棱柱.∴体积为3×2×1-2×1×1=4.答案:48.已知圆柱的底面周长为c,侧面展开图矩形的面积为S,则它的体积为________.解析:设圆柱底面半径为r,高为h,则∴r=,h=,∴V=πr2h=π×2·=.答案:9.如图,在三棱柱ABC-A1B1C1中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱ABC-A1B1C1的体积为V2,则V1∶V2=________.解析:===.答案:1∶24三、解答题10.如图,直三棱柱ABC-A1B1C1的高为6cm,底面三角形的边长分别为3cm,4cm,5cm,以上,下底的内切圆为底面,挖去一个圆柱,求剩余部分形成的几何体的表面积和体积.解: 32+42=52,∴底面是直角三角形.∴上、下底面内切圆半径r==1(cm).∴S表=(3+4+5)×6+2×-2π×12+2π×1×6=72+12-2π+12π=84+10π(cm2),V=×3×4×6-π×12×6=36-6π(cm3).故剩余部分形成几何体的表面积是84+10π(cm2),体积是36-6π(cm3).11.已知某几何体的俯视图是如图所示的矩形,主视图是一个底边长为8,高为4的等腰三角形,左视图是一个底边长为6,高为4的等腰三角形.求:(1)该几何体的体积V;(2)该几何体的侧面积S.解:由已知该几何体是一个四棱锥P-ABCD,如图所示.由已知,AB=8,BC=6,高h=4,由俯视图知底面ABCD是矩形,连接AC、BD交于点O,连接PO,则PO=4,即为棱锥的高.作OM⊥AB于M,ON⊥BC于N,连接PM、PN,则PM⊥AB,PN⊥BC.∴PM===5,PN===4.(1)V=Sh=×(8×6)×4=64.(2)S侧=2S△PAB+2S△PBC=AB·PM+BC·PN=8×5+6×4=40+24.12.(2017·全国卷Ⅲ)如图,四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直...