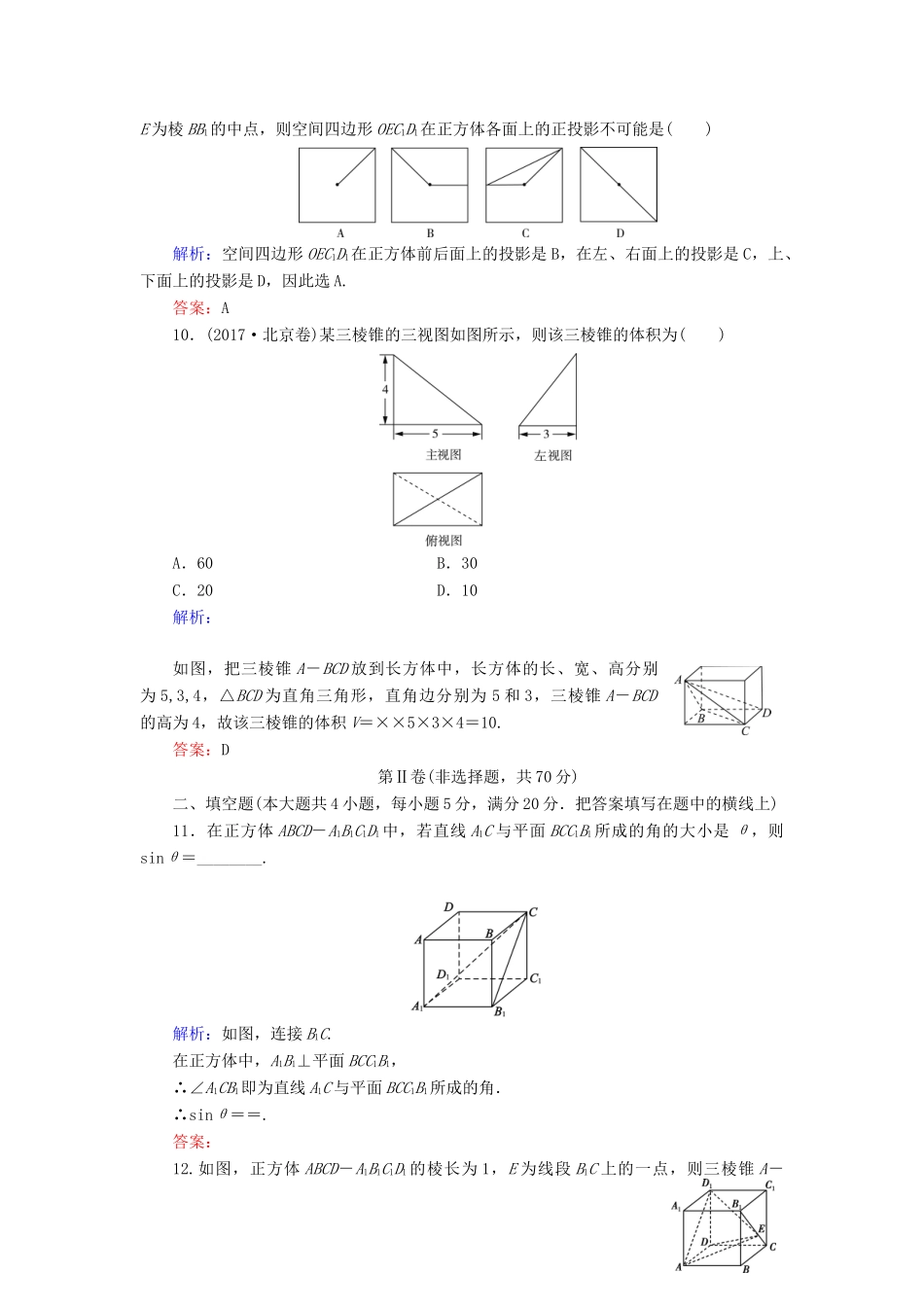
阶段性测试题一第一章立体几何初步(时间:90分钟满分:120分)第Ⅰ卷(选择题,共50分)一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在空间中,已知下列命题:①两组对应边相等,且它们的夹角也相等的两个三角形全等;②对边相等的四边形是平行四边形;③有三个角是直角的四边形是矩形;④有两组对应角相等的两个三角形相似.其中正确的是()A.①②B.③④C.②③D.①④解析:①④是平面图形,是正确的;②③在平面内正确,而在空间中不正确.答案:D2.如图,梯形A1B1C1D1是一平面图形ABCD的直观图(斜二测),若A1D1∥O1y1,A1B1∥C1D1,A1B1=C1D1=2,A1D1=1,则梯形ABCD的面积是()A.10B.5C.5D.10解析:由题意知,梯形ABCD为直角梯形,AB=2,CD=3,AD=2.∴S=×(2+3)×2=5.答案:B3.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为()A.20πB.24πC.28πD.32π解析:该几何体的表面积由圆锥的侧面积、圆柱的侧面积和圆柱的一个底面圆的面积组成.其中,圆锥的底面半径为2,母线长为=4,圆柱的底面半径为2,高为4,故所求表面积S=π×2×4+2π×2×4+π×22=28π.答案:C4.(2017·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.+1B.+3C.+1D.+3解析:由几何体的三视图可得,该几何体是由半个圆锥和一个三棱锥组成,故该几何体的体积V=×π×3+××2×1×3=+1.答案:A5.用与球心距离为1的平面去截半径为2的球,则截面面积为()A.2πB.3πC.4πD.9π解析:设球的半径为R,球心到平面的距离为h,截面圆的半径为r,则R2=r2+h2,∴r2=4-1=3,S=πr2=3π.答案:B6.已知α,β是两个不同的平面,m,n是两条不同的直线,给出下列命题:①若m⊥α,mβ,则α⊥β;②若mα,nα,m∥β,n∥β,则α∥β;③如果mα,n⃘α,m、n是异面直线,那么n与α相交;④若α∩β=m,n∥m,且n⃘α,n⃘β,则n∥α且n∥β.其中正确的命题是()A.①②B.②③C.③④D.①④解析:①满足面面垂直的判定定理,正确;②若m与n交于一点,则结论正确,否则不正确;③满足条件的n与α也可能平行;④满足线面平行的判定定理,正确.答案:D7.已知两个平面垂直,下列命题:①一个平面内已知直线必垂直于另一个平面内的任意一条直线;②一个平面内的已知直线必垂直于另一个平面的无数条直线;③一个平面内的任一条直线必垂直于另一个平面;④过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.其中正确的个数是()A.3B.2C.1D.0解析:只有②正确,①③显然不正确,对于④,当该垂线不在第一个平面内时,垂线就不垂直于另一平面.答案:C8.已知直二面角α-l-β,点A∈α,AC⊥l,C为垂足,点B∈β,BD⊥l,D为垂足.若AB=2,AC=BD=1,则CD=()A.2B.C.D.1解析:由题意得AB2=AC2+CD2+BD2,即4=1+CD2+1,解得CD=,故选C.答案:C9.如图,O为正方体ABCD-A1B1C1D1的体对角线A1C和AC1的交点,E为棱BB1的中点,则空间四边形OEC1D1在正方体各面上的正投影不可能是()解析:空间四边形OEC1D1在正方体前后面上的投影是B,在左、右面上的投影是C,上、下面上的投影是D,因此选A.答案:A10.(2017·北京卷)某三棱锥的三视图如图所示,则该三棱锥的体积为()A.60B.30C.20D.10解析:如图,把三棱锥A-BCD放到长方体中,长方体的长、宽、高分别为5,3,4,△BCD为直角三角形,直角边分别为5和3,三棱锥A-BCD的高为4,故该三棱锥的体积V=××5×3×4=10.答案:D第Ⅱ卷(非选择题,共70分)二、填空题(本大题共4小题,每小题5分,满分20分.把答案填写在题中的横线上)11.在正方体ABCD-A1B1C1D1中,若直线A1C与平面BCC1B1所成的角的大小是θ,则sinθ=________.解析:如图,连接B1C.在正方体中,A1B1⊥平面BCC1B1,∴∠A1CB1即为直线A1C与平面BCC1B1所成的角.∴sinθ==.答案:12.如图,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,则三棱锥A-DED1的体积为________.解析:VA-DED1=VE-ADD1=×1××1×1=....