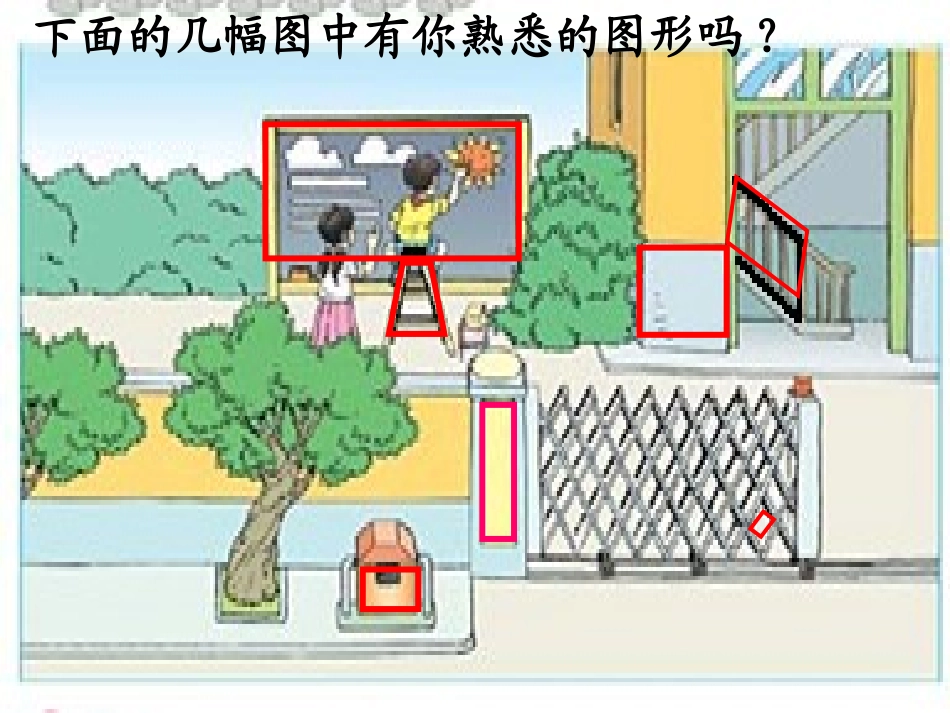
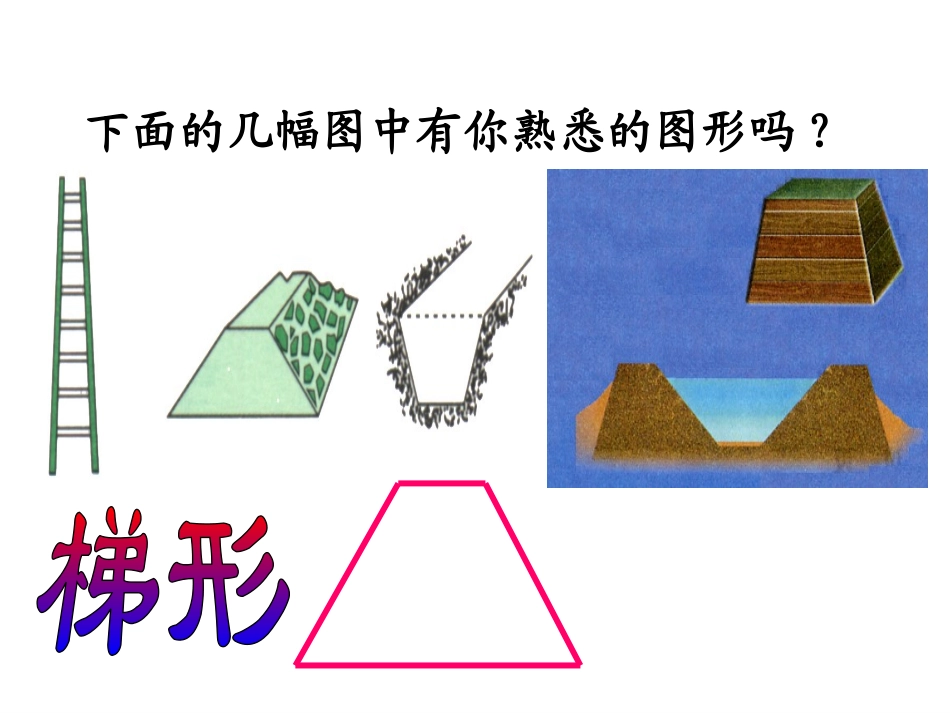
梯形下面的几幅图中有你熟悉的图形吗?下面的几幅图中有你熟悉的图形吗?1、小组商量下怎样给你准备的三角形画一条线段,使它得到一个梯形;2、然后沿你所画线段剪下来再仔细看看。活动一:画一画、剪一剪技巧:作一条边的平行线定义:一组对边平行,另一组对边不平行的四边形叫做梯形.表示方法:在梯形ABCD中,AD∥BCACDB梯形定义还可以理解成:一组对边平行且不相等的四边形是梯形下面哪些图形是梯形,为什么?1324567136是梯形如图,平行的两边叫做梯形的底,其中较短的底叫做上底,较长的底叫做下底.不平行的两边叫做腰.上底下底腰腰ACDB相关概念特殊梯形一般梯形一般三角形特殊三角形特殊三角形特殊梯形一般梯形等腰梯形:两腰相等的梯形.有两腰相等梯形等腰梯形表示方法:在梯形ABCD中,AD∥BC,AB=CDACDBACDB直角梯形:有一个角是直角的梯形.梯形有一个角是直角直角梯形CADBACDB表示方法:在梯形ABCD中,AD∥BC,∠B=90°定义:1.梯形:一组对边平行,另一组对边不平行的四边形叫做梯形.表示方法:在梯形ABCD中,AD∥BC2.等腰梯形:两腰相等的梯形.表示方法:在梯形ABCD中,AD∥BC,AB=CD3.直角梯形:有一个角是直角的梯形.表示方法:在梯形ABCD中,AD∥BC,∠B=90°4.各部分名称:上底下底腰腰ACDB活动二:折一折,画一画•请各小组分别在刚才剪出的梯形上折出或画出至少一条表示上、下底距离的线段。ACDB数学语言:过点A作BC边的垂线,垂足为E或(过点A作AEBC⊥,垂足为E).DBAC夹在两底之间的垂线段叫做梯形的高.(有无数条)EF如图,平行的两边叫做梯形的底,其中较短的底叫做上底,较长的底叫做下底.不平行的两边叫做腰,夹在两底之间的垂线段叫做梯形的高.上底下底腰腰ACDB高E相关概念活动三:折一折,叠一叠请各小组完成下列两项任务:1、用刚才所剪的等腰梯形折一折,看是不是轴对称图形,如果是,有几条对称轴,并想一想怎么用语言表达。2、折叠的过程中你有什么发现?如果画出梯形的对角线,你又有什么发现?你是怎样验证这些发现的?(可类比学平行四边形时,从边、角、对角线、对称性等角度去考虑)B试说明等腰梯形有哪些性质?从边看:两底平行两腰相等小组合作讨论从角看:同一底上的两个内角相等ACD从对角线看:从对称性看:两条对角线相等是轴对称图形,上下底中点的连线是对称轴证明:过点A作AE∥CD交BC于点E又AD∥BC∴四边形AECD是平行四边形∴AE=DC AB=DC∴AE=AB∴∠1=∠B AE∥CD∴∠1=∠C∴∠B=∠C同一底上同一底上的两个角相等ACBDE1已知:在梯形ABCD中,AD∥BC,AB=DC求证:∠B=∠C分析:通过添加辅助线,平移一腰,将梯形问题转化为平行四边形和三角形的问题来处理.归纳ACBDE1ACBDE分析:通过添加辅助线,作双高,将梯形问题转化为矩形和全等三角形的问题来处理.F归纳B从边看:两底平行两腰相等推理证明:从角看:同一底上的两个内角相等ACD从对角线看:从对称性看:两条对角线相等是轴对称图形,上下底中点的连线是对称轴等腰梯形的两条对角线将它分成的三角形中有个等腰三角形,对全等三角形23ABCDO已知:在梯形ABCD中,AD∥BC,AB=DC求证:AC=BDCABD分析:可利用刚学的等腰梯形同一底上的两个角相等,结合全等三角形性质来证明.证明:在梯形ABCD中AD∥BC AB=DC∴∠ABC=∠DCB(等腰梯形在同一底上的两个角相等)又 BC=CB∴△ABC≌△DCB(SAS)∴AC=DB等腰梯形的两条对角线相等等腰梯形的两条对角线相等B从边看:两底平行两腰相等推理证明:从角看:同一底上的两个内角相等ACD从对角线看:从对称性看:两条对角线相等是轴对称图形,上下底中点的连线是对称轴等腰梯形是轴对称图形,上下底中点的连线是对称轴.小组合作探究小组合作探究CABDB从边看:两底平行两腰相等等腰梯形的性质:从角看:同一底上的两个内角相等ACD从对角线看:从对称性看:两条对角线相等是轴对称图形,上下底中点的连线是对称轴应用、拓展:•例1如图,在等腰梯形ABCD中,AD=2,BC=4,高DF=2,求腰DC的长.你有几种方法?ABCDFABCDFEE解:将腰AB平移到DE的位置,由平移的性质和平行四边形的判别方法,可知四边形ABED是平行四边形,DE=AB=DC,BE=AD,在等腰△DEC中,EC=BC-BE=BC-...