新人教版八年级数学同底数幂的乘法课件1VIP免费

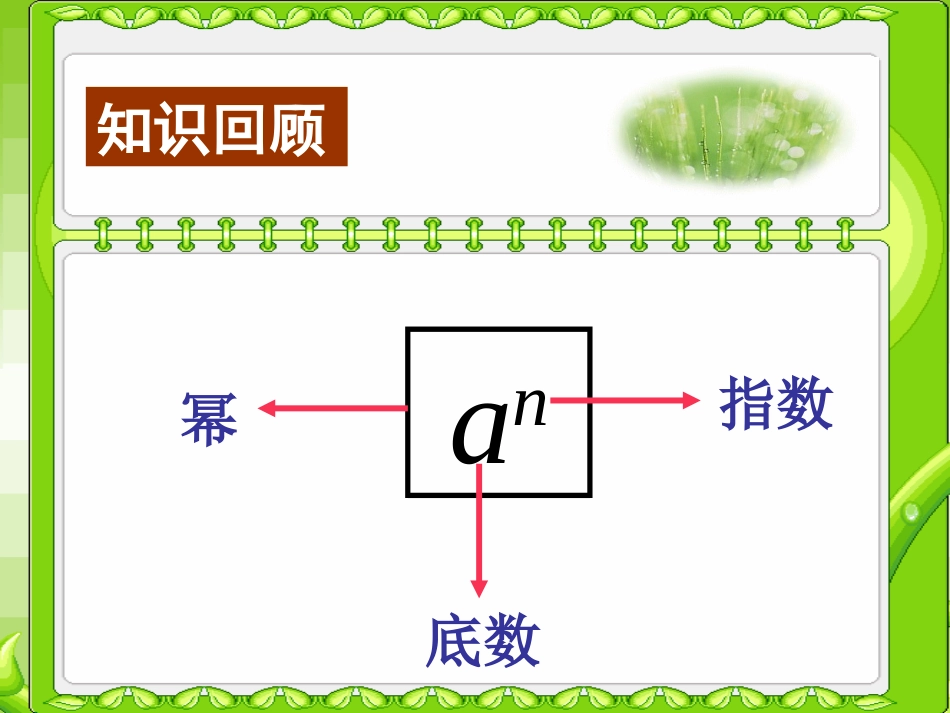
同底数幂的乘法同底数幂的乘法14.1.11、2×2×2=2()2、a·a·a·a·a=a()3、a·a······a=a()n个35n①什么叫乘方?②乘方的结果叫做什么?知识回顾an底数指数幂知识回顾说出am的乘法意义,并将下列各式写成乘法形式:(1)105(2)(-2)4=10×10×10×10×10=(-2)×(-2)×(-2)×(-2)探究新知=27(乘方的意义)(1)25×22(2)a3·a2=(2×2×2×2×2)×(2×2)(乘方的意义)=2×2×2×2×2×2×2(乘法结合律)=(=(aa··aa··aa)()(aa··aa))=a5想一想想一想你能根据乘方的意义算出下列式子的结果吗？(2)a3·a2(1)25×22(3)5m·5n(3)5m·5n=5m+n=(5×5×···×5)×(5×5×···×5)m个5n个5=5×5×······×5×5(m+n)个5想一想想一想你能根据乘方的意义算出下列式子的结果吗？(2)a3·a2(1)25×22(3)5m·5n这几道题有什么共同的特点呢?计算的结果有什么规律吗?(1)25×22=a5=27(3)5m·5n=5m+n(2)a3·a2=(=(aa··aa··aa)()(aa··aa))=(2×2×2×2×2)×(2×2)=(5×5×···×5)×(5×5×···×5)m个5n个5=25+2=a3+2想一想想一想am·an=m个an个a=aa···a=am+n(m+n)个a（aa···a）（aa···a）（乘方的意义）（乘法结合律）（乘方的意义）知识推导知识推导当m,n为正整数时，am·an=？一般地，如果m，n都是正整数，那么am·an=am+nam·an=am+n(m、n都是正整数)同底数幂相乘，底数，指数。不变相加同底数幂的乘法公式：请你尝试用文字概括这个结论。知识推导知识推导幂的底数必须相同，相乘时指数才能相加。(3)xm·x3m+1=xm+3m+1=x4m+1(1)x2.x5(2)a·a6(3)xm·x3m+1(4)解：(1)x2.x5=x2+5=x7(2)a·a6=a1+6=a7(4)2×24×23=21+4+3=28=256a=a1例1am·an=am+n43222已知：am=2，an=3.求am+n=？解：am+n=am·an=2×3=6例2=am·an=am·anam+nam+n想一想：当三个或三个以上同底数幂相乘时，是否也具有这一性质呢？怎样用公式表示？如am·an·ap=am+n+p（m、n、p都是正整数）知识拓展知识拓展知识应用辩一辩判断下列计算是否正确，并简要说明理由：（1）b5·b5=2b5（）（2）b5+b5=b10（）（3）x5·x5=x25()（4）y5·y5=2y10()（5）c·c3=c3()（6）m+m3=m4()m+m3=m+m3b5·b5=b10b5+b5=2b5x5·x5=x10y5·y5=y10c·c3=c4××××××填一填：知识应用（5）x5·（）=x8（6）a·（）=a6（7）x·x3（）=x7（8）xm·（）＝ｘ3mx3a5x3ｘ2m（1）b5·b=()（2）10·102·103=()（3）-a2·a6=()（4）y2n·yn+1＝()b6106-a8y3n+1(-2)9(a+b)7公式中的a可代表一个数、字母、式子等.知识拓展计算：(结果写成幂的形式)想一想：①(-2)4×(-2)5=②-53×(-5)2=③(a+b)2·(a+b)5=(-5)5效果检测5222,xy已知则正整数x,y的值有（）（A）1对（B）2对（C）3对（D）4对28,216,xy已知则_____2xy12.3.3D128若则的值是＿＿＿92xxxnmnm122)()(pppxxx思考计算（1）（p为正整数）（2）（n为正整数))2()2(322n同底数幂相乘，底数指数am·an=am+n(m、n正整数)小结收获小结收获我学到了什么？不变，相加。am·an·ap=am+n+p(m、n、p为正整数)am·an·ap=am+n+p(m、n、p为正整数)