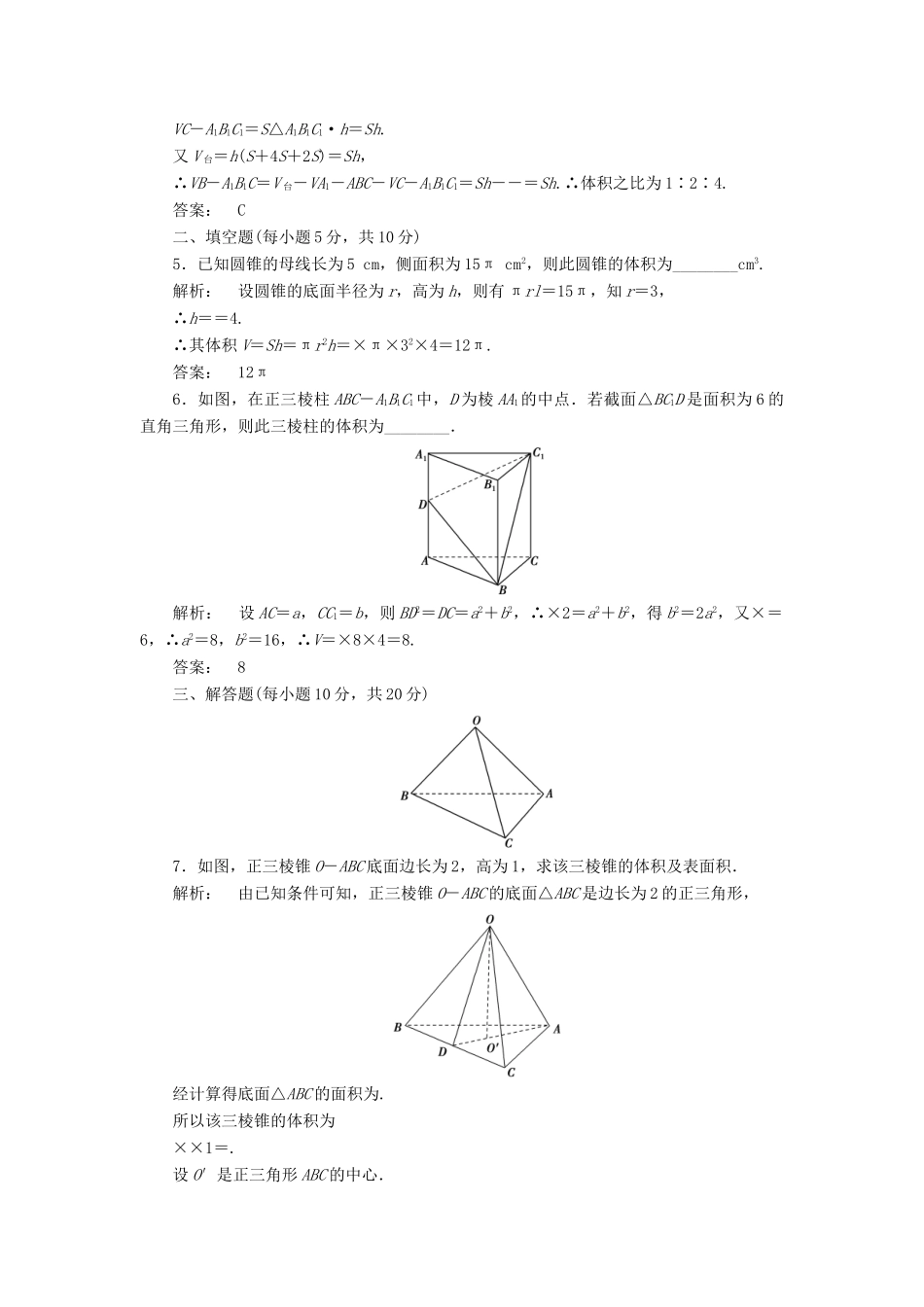
2016-2017学年高中数学第一章立体几何初步1.7.2棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积高效测评北师大版必修2一、选择题(每小题5分,共20分)1.半径为r的半圆卷成一个圆锥,则它的体积为()A.πr3B.πr3C.πr3D.πr3解析:设底面半径为r′,则2πr′=πr,∴r′=.∴圆锥的高h==r.∴V锥=πr′2×h=π××r=πr3.答案:C2.在棱长为1的正方体中,分别用过共顶点的三条棱的中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是()A.B.C.D.解析:V正方体-8V三棱锥=1-8×××××=,故选D.答案:D3.一个四棱锥的侧棱长都相等,底面是正方形,主视图如图所示,则该四棱锥侧面积和体积分别是()A.4,8B.4,C.4(+1),D.8,8解析:由题意可知该四棱锥为正四棱锥,底面边长为2,高为2,侧面上的斜高为=,所以S侧=4×=4,V=×22×2=.答案:B4.如图,三棱台ABC-A1B1C1中,AB∶A1B1=1∶2,则三棱锥A1-ABC,B-A1B1C,C-A1B1C1的体积之比为()A.1∶1∶1B.1∶1∶2C.1∶2∶4D.1∶4∶4解析:设棱台的高为h,S△ABC=S,则S△A1B1C1=4S.∴VA1-ABC=S△ABC·h=Sh.VC-A1B1C1=S△A1B1C1·h=Sh.又V台=h(S+4S+2S)=Sh,∴VB-A1B1C=V台-VA1-ABC-VC-A1B1C1=Sh--=Sh.∴体积之比为1∶2∶4.答案:C二、填空题(每小题5分,共10分)5.已知圆锥的母线长为5cm,侧面积为15πcm2,则此圆锥的体积为________cm3.解析:设圆锥的底面半径为r,高为h,则有πrl=15π,知r=3,∴h==4.∴其体积V=Sh=πr2h=×π×32×4=12π.答案:12π6.如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点.若截面△BC1D是面积为6的直角三角形,则此三棱柱的体积为________.解析:设AC=a,CC1=b,则BD2=DC=a2+b2,∴×2=a2+b2,得b2=2a2,又×=6,∴a2=8,b2=16,∴V=×8×4=8.答案:8三、解答题(每小题10分,共20分)7.如图,正三棱锥O-ABC底面边长为2,高为1,求该三棱锥的体积及表面积.解析:由已知条件可知,正三棱锥O-ABC的底面△ABC是边长为2的正三角形,经计算得底面△ABC的面积为.所以该三棱锥的体积为××1=.设O′是正三角形ABC的中心.由正三棱锥的性质可知,OO′垂直于平面ABC.延长AO′交BC于D,得AD=,O′D=.又因为OO′=1,所以正三棱锥的斜高OD=.故侧面积为×2××3=2.所以该三棱锥的表面积为+2=3.因此,所求三棱锥的体积为,表面积为3.8.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,求V1∶V2.解析:通过点D,E,F为中点得出三棱柱与三棱锥的底面面积以及高之间的关系,然后利用体积公式得到体积之间的比值.设三棱柱的底面ABC的面积为S,高为h,则其体积为V2=Sh.因为D,E分别为AB,AC的中点,所以△ADE的面积等于S.又因为F为AA1的中点,所以三棱锥F-ADE的高等于h,于是三棱锥F-ADE的体积V1=×S×h=Sh=V2,故V1∶V2=1∶24.☆☆☆9.(10分)如图是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6cm,高为20cm的圆锥形铅锤,且水面高于圆锥顶部,当铅锤从水中取出后,杯里的水将下降多少?解析:因为圆锥形铅锤的体积为×π×2×20=60π(cm3),设水面下降的高度为xcm,则小圆柱的体积为π2x=100πx.所以有60π=100πx,解此方程得x=0.6,故杯里的水将下降0.6cm.