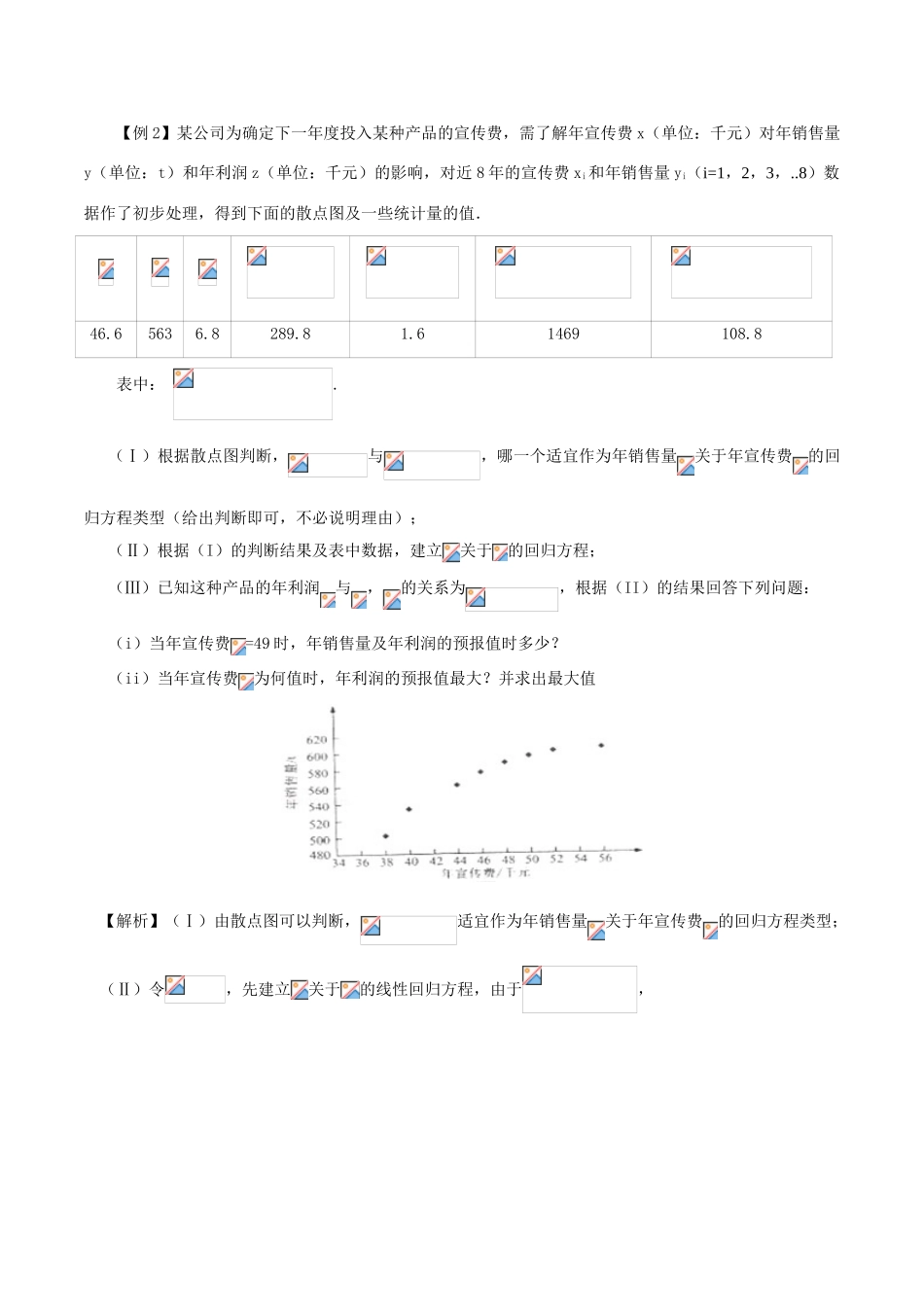
第08讲:函数方程思想情形之12-14【知识要点】一、数学思想是人对数学知识的本质认识,是从某些具体的数学内容和对数学的认识过程中提炼上升的数学观点,它在认识过程中被反复运用,带有普遍的指导意义.是建立数学和用数学解决问题的指导思想,而且数学思想是数学学科的精髓,是数学素养的重要内容之一.学生只有领会了数学思想,才能有效地应用知识,形成能力.在我们解决数学问题进行数学思维时,也总是自觉或不自觉地运用数学思想方法.高中数学解题常用的数学思想有数形结合思想、分类讨论思想、转化化归思想、函数方程思想等.二、函数是中学数学的一个重要概念,它渗透在数学各部分内容中,一直是高考的热点、重点内容.函数的思想,就是用运动变化的观点,分析和研究具体问题中的数量关系,建立函数特征,重在对问题的变量的动态研究,从变量的运动变化、联系和发展角度拓宽解题思路.方程的思想,是从问题的数量关系入手,运用数学语言讲问题中的条件转化为数学模型(方程、不等式或方程与不等式的混合组),然后通过解方程(组)或不等式(组)来使问题获解.三、函数与方程的思想在解题中的应用主要表现在两个方面:一是借助有关初等函数的性质,解有关求值、解(证)不等式、解方程以及讨论参数的取值范围等问题;二是在问题的研究中,通过建立函数关系式或构造中间函数,把所研究的问题转化为讨论函数的有关性质,达到化难为易,化繁为简的目的,有时,还实现函数与方程的互相转化,接轨,达到解决问题的目的.四、本讲讲了函数方程思想情形之12-14,情形12:复数中的函数方程思想;情形13:统计中的函数方程思想;14:实际问题中的函数方程思想.【方法讲评】函数方程情形十二复数中的函数方程思想复数中,与复数实部、虚部、复数的模等求值有关的计算,多利用方程的思想解答.与取值范围、最值有关的问题,多利用函数的思想分析解答,先建立函数的模型,再研究函数的取值范围和最值.【例1】设z是虚数,是实数,且.(1)求的值及z的实部的取值范围.(2)设,求的最小值.【解析】(1)设且,则 是实数,∴,又是虚数,∴,∴,即,∴, ,∴,即,故z的实部取值范围;【点评】(1)本题第1问求的值,利用了方程的思想.(2)本题第2问求的最小值,利用了函数的思想,先建立函数的模型,再利用基本不等式求函数的最小值.可见,函数思想是无处不在的,特别是与最值、取值范围和值域有关的问题,更要想到函数的思想来分析解答.【反馈检测1】设复数z满足4z+2=3+i,ω=sinθ-icosθ(θ∈R).求z的值和|z-ω|的取值范围.函数方程情形十三统计中的函数方程思想统计中的最值问题,多用函数的思想分析解答,先建立函数的模型,再研究函数的取值范围和最值.【例2】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费xi和年销售量yi(i=1,2,3,..8)数据作了初步处理,得到下面的散点图及一些统计量的值.46.65636.8289.81.61469108.8表中:.(Ⅰ)根据散点图判断,与,哪一个适宜作为年销售量关于年宣传费的回归方程类型(给出判断即可,不必说明理由);(Ⅱ)根据(I)的判断结果及表中数据,建立关于的回归方程;(Ⅲ)已知这种产品的年利润与,的关系为,根据(II)的结果回答下列问题:(i)当年宣传费=49时,年销售量及年利润的预报值时多少?(ii)当年宣传费为何值时,年利润的预报值最大?并求出最大值【解析】(Ⅰ)由散点图可以判断,适宜作为年销售量关于年宣传费的回归方程类型;(Ⅱ)令,先建立关于的线性回归方程,由于,(ii)根据(Ⅱ)的结果可知,年利润z的预报值=0.2(100.6+68)﹣=﹣+13.6+20.12,当==6.8,即=46.24千元时,年利润的预报值最大.【点评】(1)本题第2问建立关于的回归方程,利用了方程的思想.(2)本题的第3问求年利润的预报值最大值,利用了函数的思想,先建立函数模型年利润z的预报值=﹣+13.6+20.12,再利用二次函数求函数的最大值.【反馈检测2】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:(...