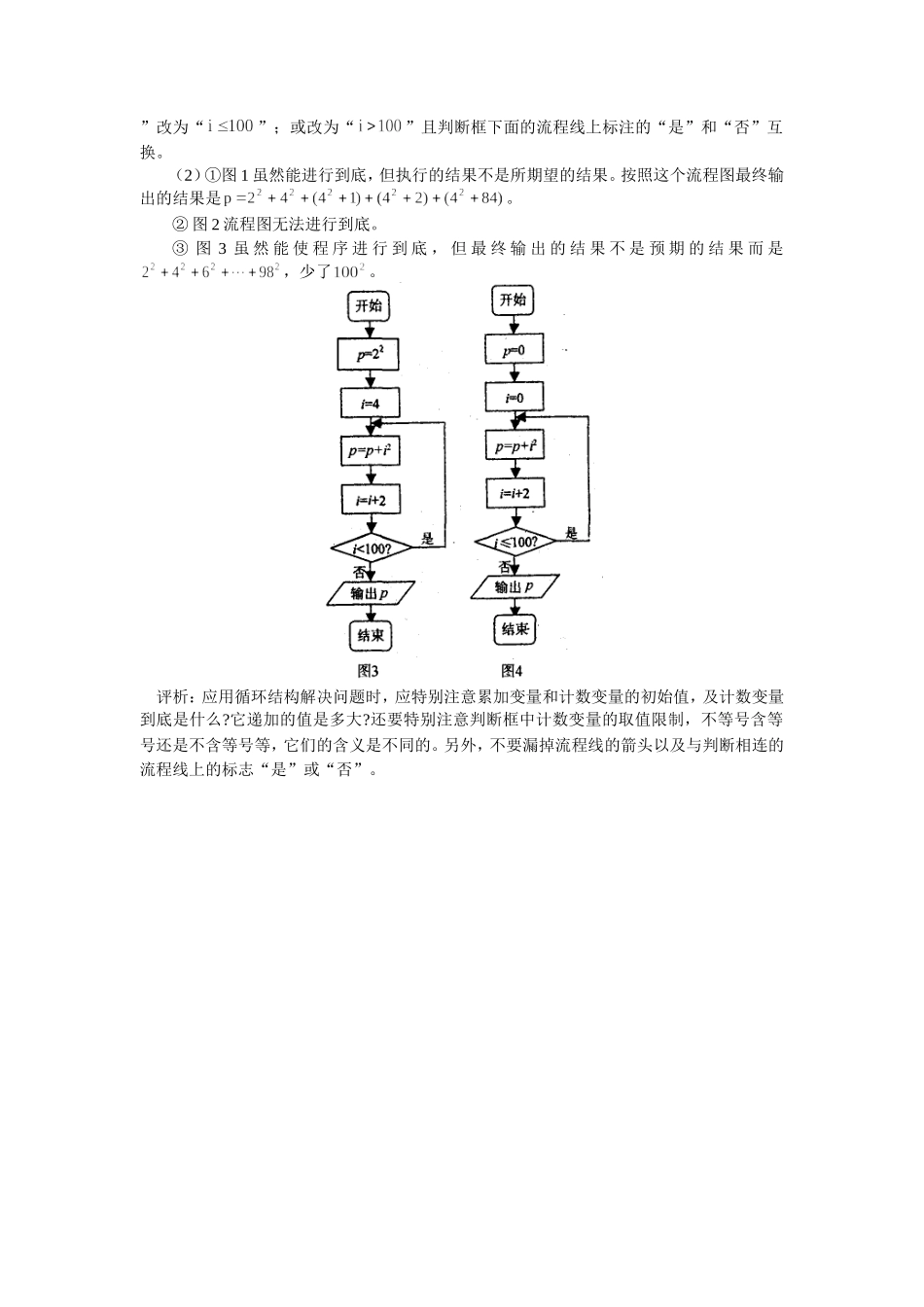
理解框图的基本逻辑结构体会算法的程序化思想随着现代信息技术的飞速发展,算法在科学技术、社会发展中发挥着越来越大的作用,并日益融入社会生活的许多方面,算法思想已经成为现代人应具备的一种数学素养。下面通过对解决具体问题过程与步骤的分析,理解程序框图的三种基本逻辑结构,体会算法的程序化思想。例:下列是为计算而绘制的算法流程图,根据流程图回答:(1)其中正确的流程图有哪几个?错误的流程图有哪几个?错误的要指出错在哪里。(2)错误的流程图中,按该流程图所蕴含的算法,能执行到底吗?若能执行到底,最后输出的结果是什么?解析:(1)正确的流程图只有图4。①图l有三处错误。第一处错误:第二个图框中,应该是,因为本流程图中的计数变量是i,不是。在中,指数都是2,而底数2,4,6,8,…,100是变化的,但前后两项的底数相差2,因此计数变量是顺加2。第二处错误:第三个图框中的内容错误,累加的是而不是,故应改为。第三处错误:第四个图框中的内容,其中的指令,应改为,原因是底数前后两项相差2。②图2所示的流程图中共有四处错误。第一处错误:流程线没有箭头显示程序的执行顺序。第二处错误:第三个图框中的内容p=p+i错,应改为p=p+i2。.第三处错误:判断框的流程线上没有标明“是”或“否”,应在向下的流程线上注明“是”,在向右的流程线上标注“否”。第四处错误:在第三个图框和判断过程中漏掉了循环体中起主要作用的框图,内容即为i=i+2,使程序无法退出循环,应在第三个图框和判断框之间添加图框。③图3所示的流程图中有一处错误,即判断框中的内容错误,应将框内的内容“”改为“”;或改为“”且判断框下面的流程线上标注的“是”和“否”互换。(2)①图1虽然能进行到底,但执行的结果不是所期望的结果。按照这个流程图最终输出的结果是。②图2流程图无法进行到底。③图3虽然能使程序进行到底,但最终输出的结果不是预期的结果而是,少了。评析:应用循环结构解决问题时,应特别注意累加变量和计数变量的初始值,及计数变量到底是什么?它递加的值是多大?还要特别注意判断框中计数变量的取值限制,不等号含等号还是不含等号等,它们的含义是不同的。另外,不要漏掉流程线的箭头以及与判断相连的流程线上的标志“是”或“否”。