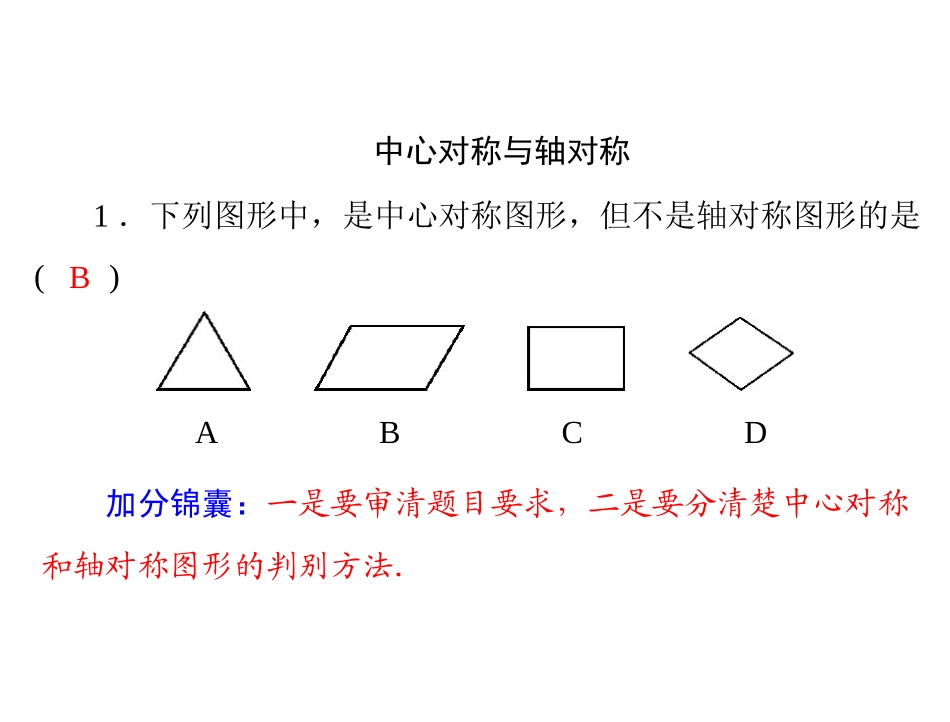
第六章易错题集中心对称与轴对称1.下列图形中,是中心对称图形,但不是轴对称图形的是()BABCD加分锦囊:一是要审清题目要求,二是要分清楚中心对称和轴对称图形的判别方法.相似三角形2.已知△ABC中,AB=8,BC=7,AC=6,点D,E分别在AB,AC上,如果以A,D,E为顶点的三角形和以A,B,C为顶点的三角形相似,且相似比为14,试求AD和AE的长.(1)如图D67(1),当△ADE∽△ABC时,由相似三角形对应边的比等于相似比知:ADAB=AEAC=14,即AD8=AE6=14.所以AD=2,AE=1.5.(1)(2)图D67(2)如图D67(2),当△AED∽△ABC时,由相似三角形对应边的比等于相似知:ADAC=AEAB=14,即AD6=AE8=14.所以AD=1.5,AE=2.加分锦囊:题中所给出的以A,D,E为顶点的三角形和以A,B,C为顶点的三角形相似,仅表明两个三角形具有相似关系,因此,应分类讨论.不能定势地认为是ΔADE∽△ABC.投影的应用3.某同学想测量旗杆的高度,他在某一时刻测得1m长的竹竿竖起放置时影长为1.5m,在同一时刻测量旗杆的影长时,因旗杆靠近一幢楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21m,留在墙上的影高位2m(如图6-1),求旗杆的高度.图6-1加分锦囊:误认为旗杆影子落在墙壁上的长即为该部分落在地面上的影长,从而导致错误.解:作CE⊥AB于点E.∵DC⊥BD于D,AB⊥BD于B,∴四边形BDCE为矩形.∴CE=BD=21m,BE=DC=2m.∵同一时刻物高与影长所组成的三角形相似,∴11.5=AE21.解得AE=14m.∴AB=14+2=16(m).所以旗杆高16m.