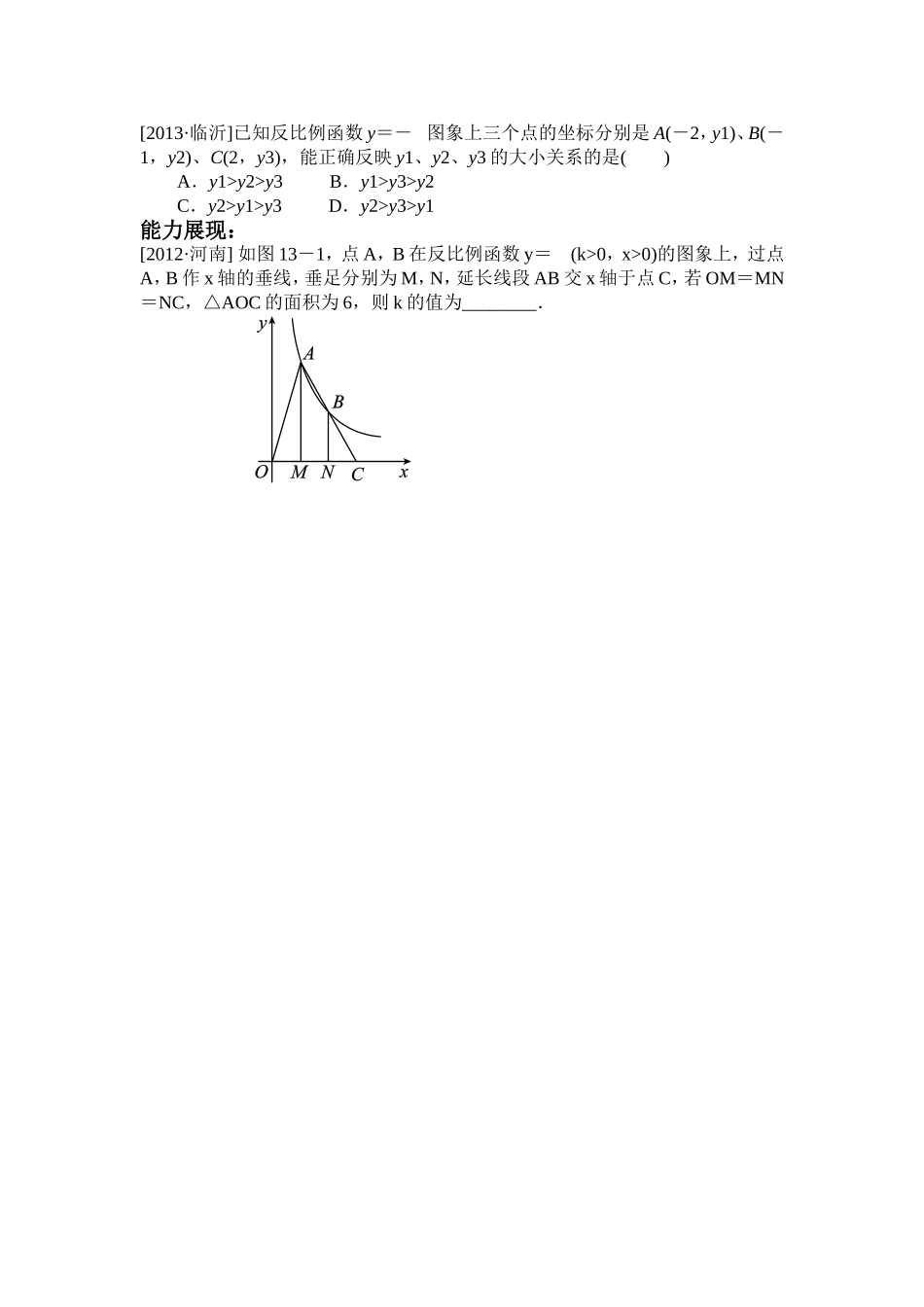
反比例函数中考复习复习目标1、结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的解析式。2、能画出反比例函数的图象,根据图象和解析式y=(k≠0)探索并理解k>0和k<0时,图象的变化情况。3、理解反比例函数的性质,能利用性质解题。4、会用待定系数法求反比例函数的解析式;能综合利用一次函数与反比例函数的性质解题。知识梳理反比例函数的定义:1、一般地,形如y=(k为常数,k_______0)的函数叫做反比例函数。反比例函数的性质:2、反比例函数y=(k≠0)的图象是_______.当k>0时,两分支分别位于第_______象限内,且在每个象限内,y随x的增大而_______;当k<0时,两分支分别位于第_______象限内,且在每个象限内,y随x的增大而_______。3、反比例函数的图象是中心对称图形,其对称中心为_______;反比例函数还是_______图形,它有两条_______,分别是_______。4、在双曲线y=上任取一点P向两坐标轴作垂线,与两坐标轴围成的矩形的面积等于_______。5、因为在反比例函数的关系式y=(k≠0)中,只有一个待定系数k,确定了k的值,也就确定了反比例函数的关系式,因而一般只要给出一组x、y的值或图象上任意一点的坐标,然后代入y=中即可求出_______的值,进而确定出反比例函数的关系式。归类示例类型之一反比例函数的概念命题角度:1.反比例函数的概念;2.求反比例函数的解析式.例1[2013·扬州]某反比例函数的图象经过(-1,6),则下列各点中,此函数图象也经过的点是()A.(-3,2)B.(3,2)C.(2,3)D.(6,1)同步检测:1.有一个面积为40的三角形,设它的底是x,高为y,则y与x的函数关系式是_____。2.已知y与x成反比例,又知当x=2时,y=3,则y与x的函数关系式是:______。3.若函数52)2(kxky是反比例函数,则k=_____。类型之二反比例函数的图象与性质命题角度:1.反比例函数的图象与性质;kxkxkx2.反比例函数中k的几何意义.例2[2013·兰州]在反比例函数y=(k<0)的图象上有两点,,则y1-y2的值是()A.负数B.非正数C.正数D.不能确定例3(’15陕西)如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=4/x的图象交于A、B两点,则四边形MAOB的面积为__________.类型之三反比例函数的应用命题角度:1.反比例函数在实际生活中的应用;2.反比例函数与一次函数的综合运用.例4(’15兰州)在同一直角坐标系中,一次函数y=kx-k与反比例函数y=k/x(k≠0)的图象可能是()例5(’15攀枝花)如图,已知一次函数y1=k1x+b的图象与x轴、y轴分别交于A、B两点,与反比例函数y2=k2/x的图象分别交于C、D两点,点D(2,-3),点B是线段AD的中点.(1)求一次函数y1=k1x+b与反比例函数y2=k2/x的解析式;(2)求△COD的面积;(3)直接写出y1>y2时自变量x的取值范围.回归教材比较反比例函数值的大小方法多例6:已知点A(-2,y1)、B(1,y2)和C(2,y3)都在反比例函数y=(k<0)的图象上,那么y1、y2和y3的大小关系如何?中考变式[2013·临沂]已知反比例函数y=-图象上三个点的坐标分别是A(-2,y1)、B(-1,y2)、C(2,y3),能正确反映y1、y2、y3的大小关系的是()A.y1>y2>y3B.y1>y3>y2C.y2>y1>y3D.y2>y3>y1能力展现:[2012·河南]如图13-1,点A,B在反比例函数y=(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,△AOC的面积为6,则k的值为________.