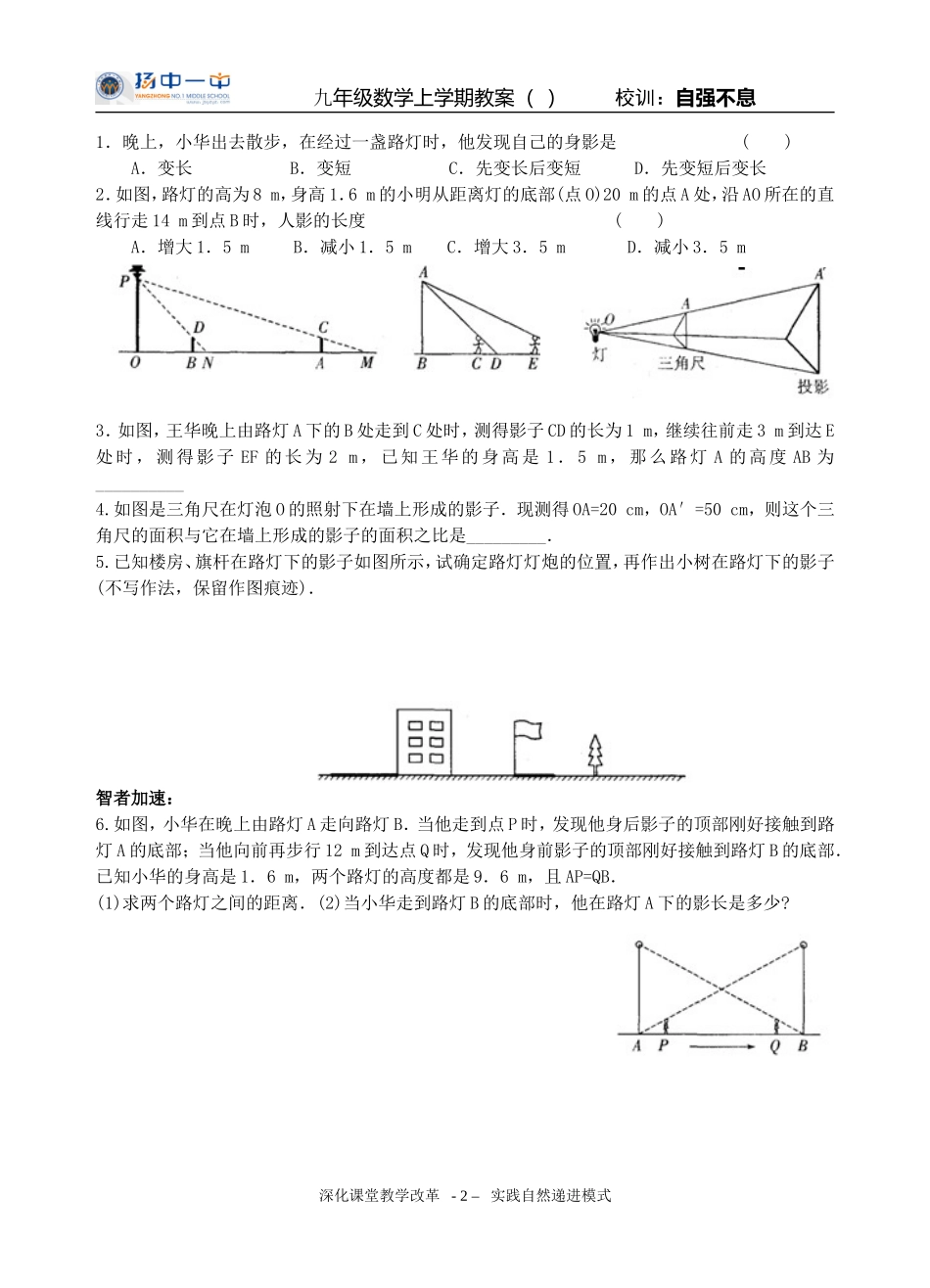
九年级数学上学期教案()校训:自强不息第46课时用相似三角形解决问题(2)主备人:何敏上课时间:审核人:杨卫国班级:_____________姓名:_______________审批人:教学目标:1.了解中心投影的意义.2.通过测量活动,综合运用判定三角形相似的条件和三角形相似的性质解决问题,通过操作、观察等数学活动,探究中心投影与平行投影的区别,并运用中心投影的相关知识解决一些实际问题.教学重点和难点:重点:综合运用定三角形相似的性质解决问题.难点:用中心投影的相关知识解决一些实际问题.教学过程:一、自主尝试1.在同一时刻物高与影长成比例,小华量得综合楼的影长为6米,同一时刻她量得身高1.6米的同学的影长为0.6米,则可知综合楼高为米.2.如图是测量旗杆的方法.已知AB是标杆,BC表示AB在太阳光下的影子,则下列叙述错误的是()A.可以利用在同一时刻,不同物体与其影长的比相等来计算旗杆的高B.可以利用△ABC∽△EDB来计算旗杆的高C.只需测量出标杆和旗杆的影长就可计算出旗杆的高D.需要测量出AB、BC和DB的长,才能计算出旗杆的高二、互动探究例1如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小明得身高为1.6m,求路灯杆AB的高度。例2如图,小明晚上在路灯下散步,已知小明的身高AB=h,灯柱的高OP=O’P’=L,两灯柱之间的距离OO’=m.(1)若小明距离灯柱OP的水平距离OA=a,求他的影子AC的长;(2)若小明在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值?请说明理由。三、反馈检测(10分钟)深化课堂教学改革-1–实践自然递进模式AO’DCOPP’B九年级数学上学期教案()校训:自强不息1.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是()A.变长B.变短C.先变长后变短D.先变短后变长2.如图,路灯的高为8m,身高1.6m的小明从距离灯的底部(点O)20m的点A处,沿AO所在的直线行走14m到点B时,人影的长度()A.增大1.5mB.减小1.5mC.增大3.5mD.减小3.5m3.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1m,继续往前走3m到达E处时,测得影子EF的长为2m,已知王华的身高是1.5m,那么路灯A的高度AB为__________4.如图是三角尺在灯泡O的照射下在墙上形成的影子.现测得OA=20cm,OA′=50cm,则这个三角尺的面积与它在墙上形成的影子的面积之比是_________.5.已知楼房、旗杆在路灯下的影子如图所示,试确定路灯灯炮的位置,再作出小树在路灯下的影子(不写作法,保留作图痕迹).智者加速:6.如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.(1)求两个路灯之间的距离.(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?深化课堂教学改革-2–实践自然递进模式