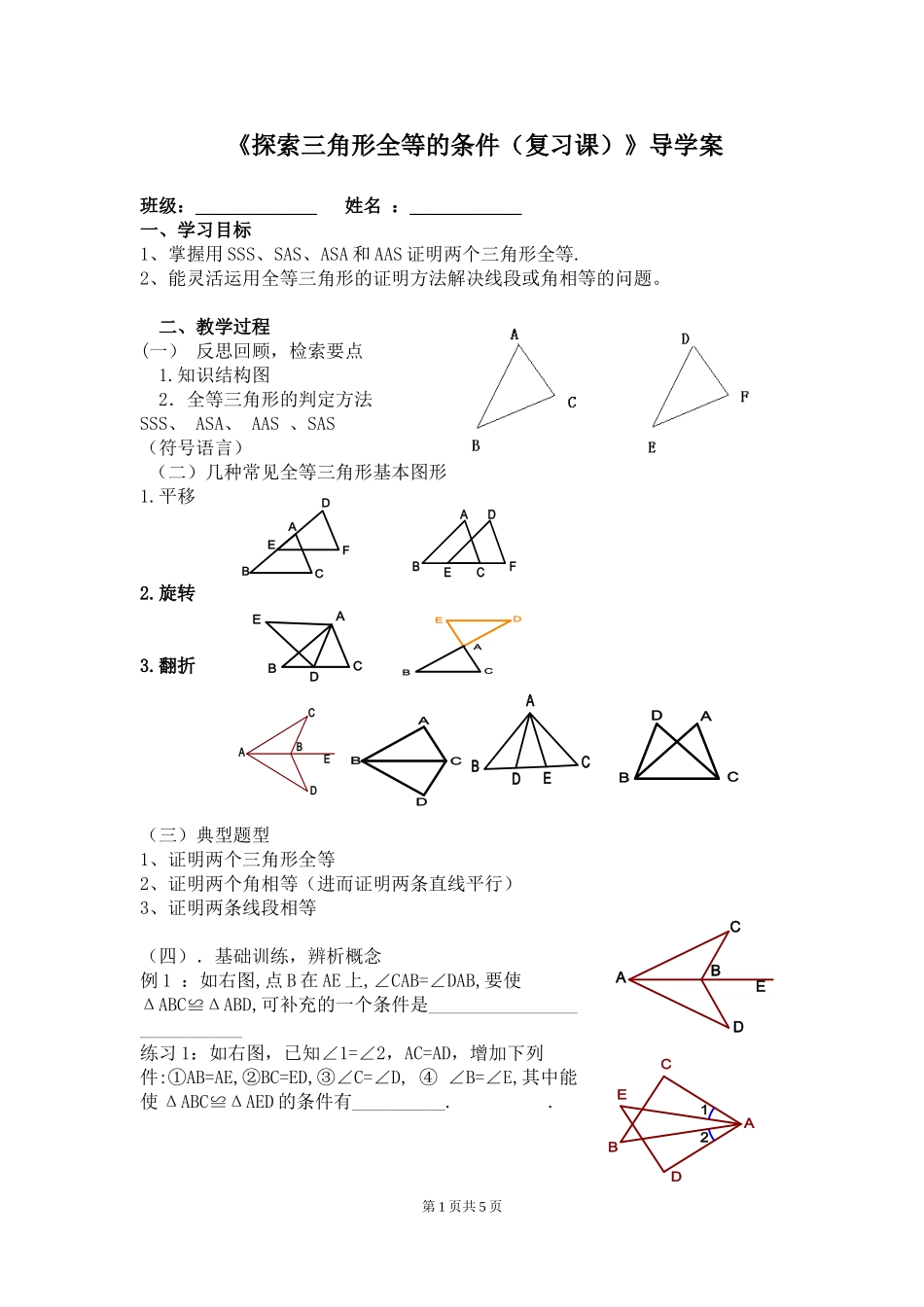
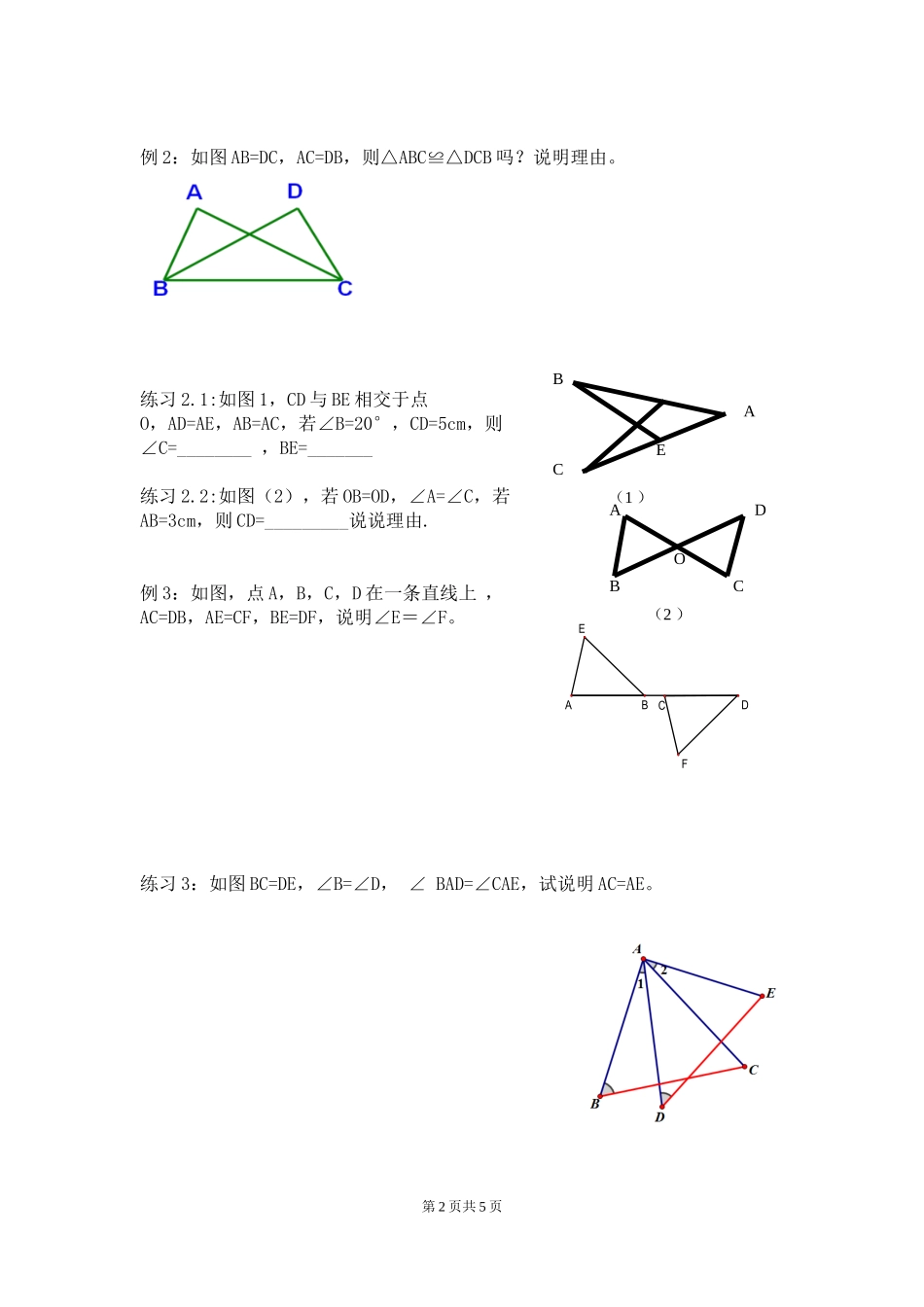
EDCBAEDCBA《探索三角形全等的条件(复习课)》导学案班级:_____________姓名:____________一、学习目标1、掌握用SSS、SAS、ASA和AAS证明两个三角形全等.2、能灵活运用全等三角形的证明方法解决线段或角相等的问题。二、教学过程(一)反思回顾,检索要点1.知识结构图2.全等三角形的判定方法SSS、ASA、AAS、SAS(符号语言)(二)几种常见全等三角形基本图形1.平移2.旋转3.翻折(三)典型题型1、证明两个三角形全等2、证明两个角相等(进而证明两条直线平行)3、证明两条线段相等(四).基础训练,辨析概念例1:如右图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是___________________________练习1:如右图,已知∠1=∠2,AC=AD,增加下列件:①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,其中能使ΔABC≌ΔAED的条件有__________..第1页共5页FEDCBAFEDCBAEDCBA21EDCBADCBADCBAEDCBAEDCBAEABDCF例2:如图AB=DC,AC=DB,则△ABC≌△DCB吗?说明理由。练习2.1:如图1,CD与BE相交于点O,AD=AE,AB=AC,若∠B=20°,CD=5cm,则∠C=________,BE=_______练习2.2:如图(2),若OB=OD,∠A=∠C,若AB=3cm,则CD=_________说说理由.例3:如图,点A,B,C,D在一条直线上,AC=DB,AE=CF,BE=DF,说明∠E=∠F。练习3:如图BC=DE,∠B=∠D,∠BAD=∠CAE,试说明AC=AE。第2页共5页(2)DAOBCBCEA(1)例4.(“三月三,放风筝”)如图是小东同学自己做的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC。请用所学的知识给予说明。练习4:已知AB=AC,OB=OC,(1)说明BD=CE;(2)说明OD=OE(五)归纳小结1.找全等三角形的方法:(1)可以从结论出发,看要证明相等的两条线段(或两个角)分别在哪两个可能全等的三角形中;(2)可以从已知条件出发,看已知条件可以确定哪两个三角形相等;(3)从条件和结论综合考虑,看它们能一同确定哪两个三角形全等.2.证明三角形全等常用的方法:(1)挖掘“隐含条件”判全等;(2)转化“间接条件”判全等;(3)添条件判全等。3.判定三角形全等的基本思路第3页共5页21ABDCEMBCAEFEAOBCD四、课后作业1.如图,在△ABC和△BAD中,,请你再补充一个条件,使△ABC≌△BAD.你补充的条件是(只填一个即可).2.已知点B是线段AC的中点,BD=BE,∠1=∠2,试说明△ADB和△CEB全等。3.如图,已知点M是△ABC的边BC上的一点,点E、F在射线AE上,BE∥CF,且BE=CF,求证:BM=MC4.已知AB=AC,AD=AE,(1)说明BD=CE;(2)说明OD=OE第4页共5页CABD第5页共5页