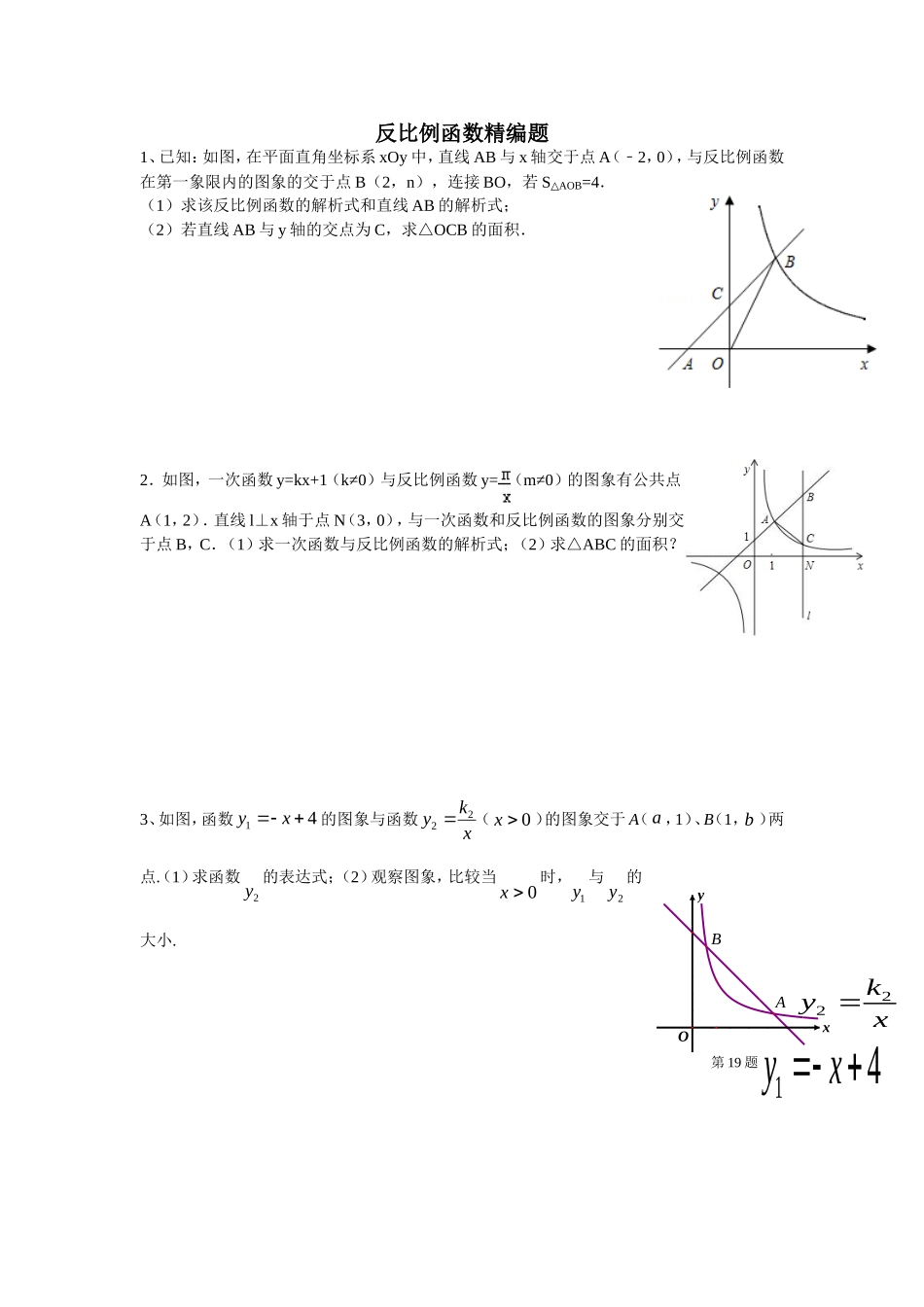
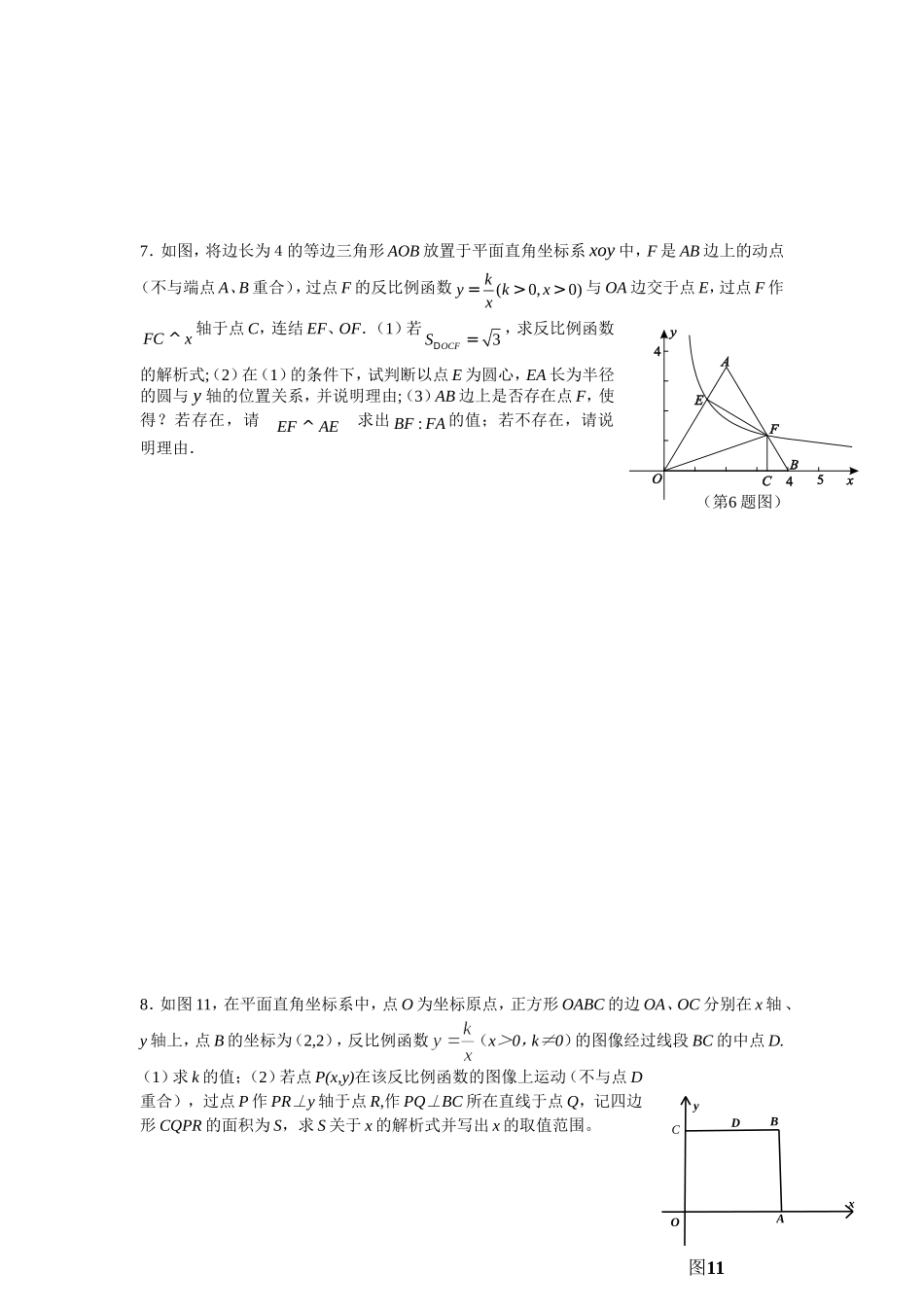
xyO第19题AB14yxxky22反比例函数精编题1、已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连接BO,若SAOB△=4.(1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与y轴的交点为C,求△OCB的面积.2.如图,一次函数y=kx+1(k≠0)与反比例函数y=(m≠0)的图象有公共点A(1,2).直线l⊥x轴于点N(3,0),与一次函数和反比例函数的图象分别交于点B,C.(1)求一次函数与反比例函数的解析式;(2)求△ABC的面积?3、如图,函数14yx的图象与函数xky22(0x)的图象交于A(a,1)、B(1,b)两点.(1)求函数2y的表达式;(2)观察图象,比较当0x时,1y与2y的大小.4、如图,在平面直角坐标系中,点A(-3,4)关于轴的对称点为B,连结AB,反比例函数的图象经过点B,过点B作BC⊥轴于点C;点P是该反比例函数图象上的任意一点,过点P作PD⊥轴于点D,连结OP,点Q是线段AB上任意一点,连结OQ,CQ。(1)求的值;(2)判断△QOC与△POD的面积是否相等,并说明理由。5、如图,直线y=k1x+b(k1≠0)与双曲线y=(k2≠0)相交于A(1,m)、B(﹣2,﹣1)两点.(1)求直线和双曲线的解析式.(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)为双曲线上的三点,且x1<x2<0<x3,请直接写出y1,y2,y3的大小关系式.6.已知点O是坐标系的原点,直线y=-x+m+n与双曲线y=交于两个不同的点A(m,n)(m≥2)和B(p,q),直线y=-x+m+n与y轴交于点C,求△OBC的面积S的取值范围.7.如图,将边长为4的等边三角形AOB放置于平面直角坐标系xoy中,F是AB边上的动点(不与端点A、B重合),过点F的反比例函数(0,0)kykxx=>>与OA边交于点E,过点F作FCx^轴于点C,连结EF、OF.(1)若3OCFSD=,求反比例函数的解析式;(2)在(1)的条件下,试判断以点E为圆心,EA长为半径的圆与y轴的位置关系,并说明理由;(3)AB边上是否存在点F,使得?若存在,请求出:BFFA的值;若不存在,请说明理由.8.如图11,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数(x>0,k≠0)的图像经过线段BC的中点D.(1)求k的值;(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。(第6题图)ACxBD图11yOEFAE^9.已知反比例函数的图象与一次函数图象交于A、B两点,连结AO。(1)求反比例函数和一次函数的表达式;(2)设点C在y轴上,且与点A、O构成等腰三角形,请直接写出点C的坐标。