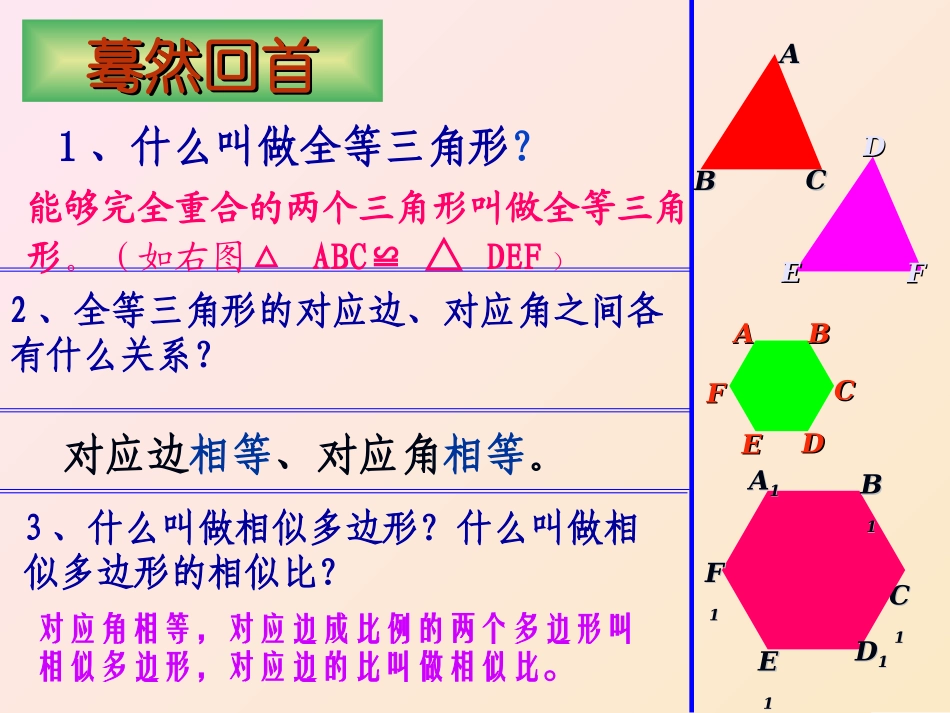
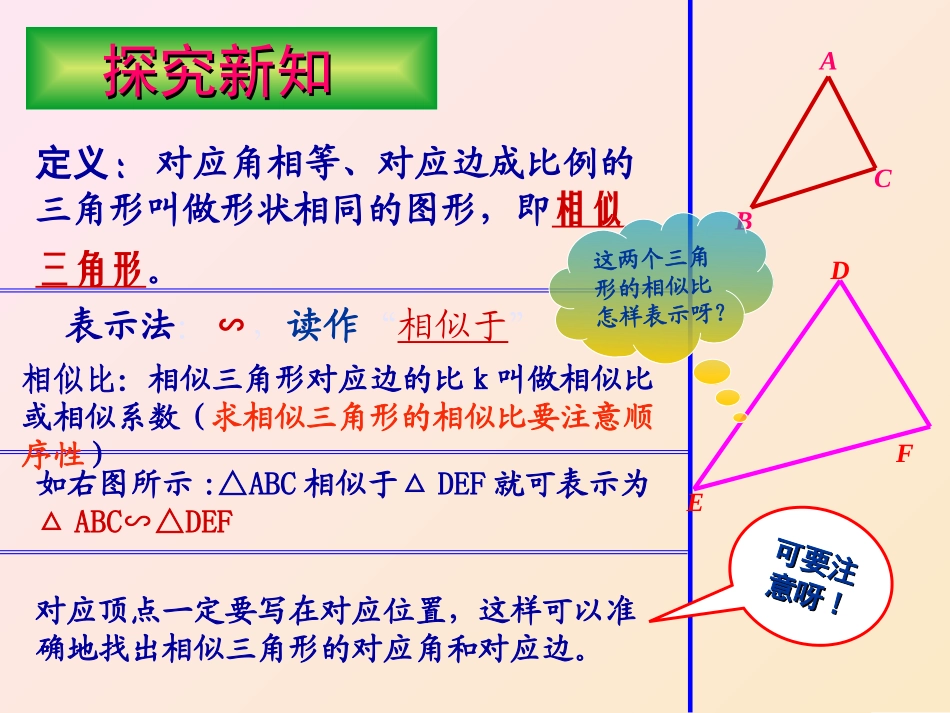
相似三角形相似三角形蓦然回首蓦然回首1、什么叫做全等三角形?能够完全重合的两个三角形叫做全等三角形。(如右图△ABC≌△DEF)2、全等三角形的对应边、对应角之间各有什么关系?对应边相等、对应角相等。3、什么叫做相似多边形?什么叫做相似多边形的相似比?对应角相等,对应边成比例的两个多边形叫相似多边形,对应边的比叫做相似比。AABBCCDDEEFFAACC11AA11BB11DD11EE11FF11BBCCDDEEFF探究新知探究新知定义:对应角相等、对应边成比例的三角形叫做形状相同的图形,即相似三角形。ABCEDF表示法:∽,读作“相似于”如右图所示:△ABC相似于△DEF就可表示为△ABC∽△DEF对应顶点一定要写在对应位置,这样可以准确地找出相似三角形的对应角和对应边。可要注可要注意呀意呀!!相似比:相似三角形对应边的比k叫做相似比或相似系数(求相似三角形的相似比要注意顺序性)这两个三角形的相似比怎样表示呀?11、如图所示如果△、如图所示如果△ADE∽△ACBADE∽△ACB,那么哪些角是对,那么哪些角是对应角?哪些边是对应边?对应角有什么关系?对应边应角?哪些边是对应边?对应角有什么关系?对应边呢?呢?想一想想一想22、如果△、如果△ABC∽△AABC∽△A11BB11CC11,,△△AA11BB11CC11∽△A∽△A22BB22CC22,,那么△那么△ABCABC与△与△AA22BB22CC22相似吗?为什么?由此可得相似三角形相似吗?为什么?由此可得相似三角形有什么性质?有什么性质?相似三角形具有传递性相似三角形具有传递性AEDCB例例11:有一块呈三角形形状的草坪,其中一边的长是:有一块呈三角形形状的草坪,其中一边的长是20m20m,在这个草坪的图纸上,这条边长,在这个草坪的图纸上,这条边长5cm5cm,其他两,其他两边的长都是边的长都是3.5cm3.5cm,求该草坪其他两边的实际长度。,求该草坪其他两边的实际长度。思考下列问题思考下列问题:1:1、草坪的形状与其图纸上相应的形、草坪的形状与其图纸上相应的形状是否相似状是否相似?2.?2.它们的相似比是多少?它们的相似比是多少?例例22:如图,已知△:如图,已知△ABC∽ADEABC∽ADE,,AEAE=50cm=50cm,,EC=30cmEC=30cm,,BC=70cmBC=70cm,∠,∠BABAC=45C=4500,∠,∠ACB=40ACB=4000,求⑴∠,求⑴∠ADEADE和和∠∠AEDAED的度数;⑵的度数;⑵DEDE的长的长AABBCCDDEE运用知识,拓展思维50cm30cm70cm450400?解:设其他两边的实际长度都是xcm,则X=3.5×400=1400cm=14m答:草坪其他两边的实际长度都是14m14005.3x20mxm5cm3.5cm3.5cm5cmAABBCCDDEE想一想:在上述的条件下,线段DE与BC平行吗?为什么?图中有哪些线段成比例?ABDBACECDBADECAEBCDEABADACAE,,例例22:如图,已知△:如图,已知△ABC∽ADEABC∽ADE,,AEAE=50cm=50cm,,EC=30cmEC=30cm,,BC=70cmBC=70cm,∠,∠BABAC=45C=4500,∠,∠ACB=40ACB=4000,求⑴∠,求⑴∠ADEADE和和∠∠AEDAED的度数;⑵的度数;⑵DEDE的长的长随堂练习,巩固新知一、在下面的两组图形中,各有两个相似三角形,试确定x、y、m、n的值x20223348303a10800450n02a450550m0y二、请同学们细心判一判1、如果两个三角形全等,则它们必相似。2、若两个三角形相似,且相似比为1,则它们必全等。3、如果两个三角形与第三个三角形相似,则这两个三角形必相似。4、相似的两个三角形一定大小不等。试一试身手一、填一填:1、如果两个三角形的相似比为1,那么这两个三角形_____2、若△ABC与△A′B′C′相似,一组对应边的长为AB=3cm,A′B′=4cm,那么△A′B′C′与△ABC的相似比是____3、若△ABC的三条边长的比为3cm、5cm、6cm,与其相似的另一个△A′B′C′的最小边长为12cm,那么A′B′C′的最大边长是_____4、已知△ABC的三条边长3cm,4cm,5cm,△ABC∽△A1B1C1,那么△A1B1C1的形状是______,又知△A1B1C1的最大边长为25cm,那么△A1B1C1的面积为全等4︰324cm直角三角形150cm2二、认真选一选1、下列命题错误的是()A.两个全等的三角形一定相似B.两个直角三角形一定相似C.两个相似三角形的对应角相等,对应边成比例D.相似的两个三角形不一定全等2、若△ABC∽△DEF,它们的周长分别为6cm和8cm,那么下式中一定成立的是()A.3...