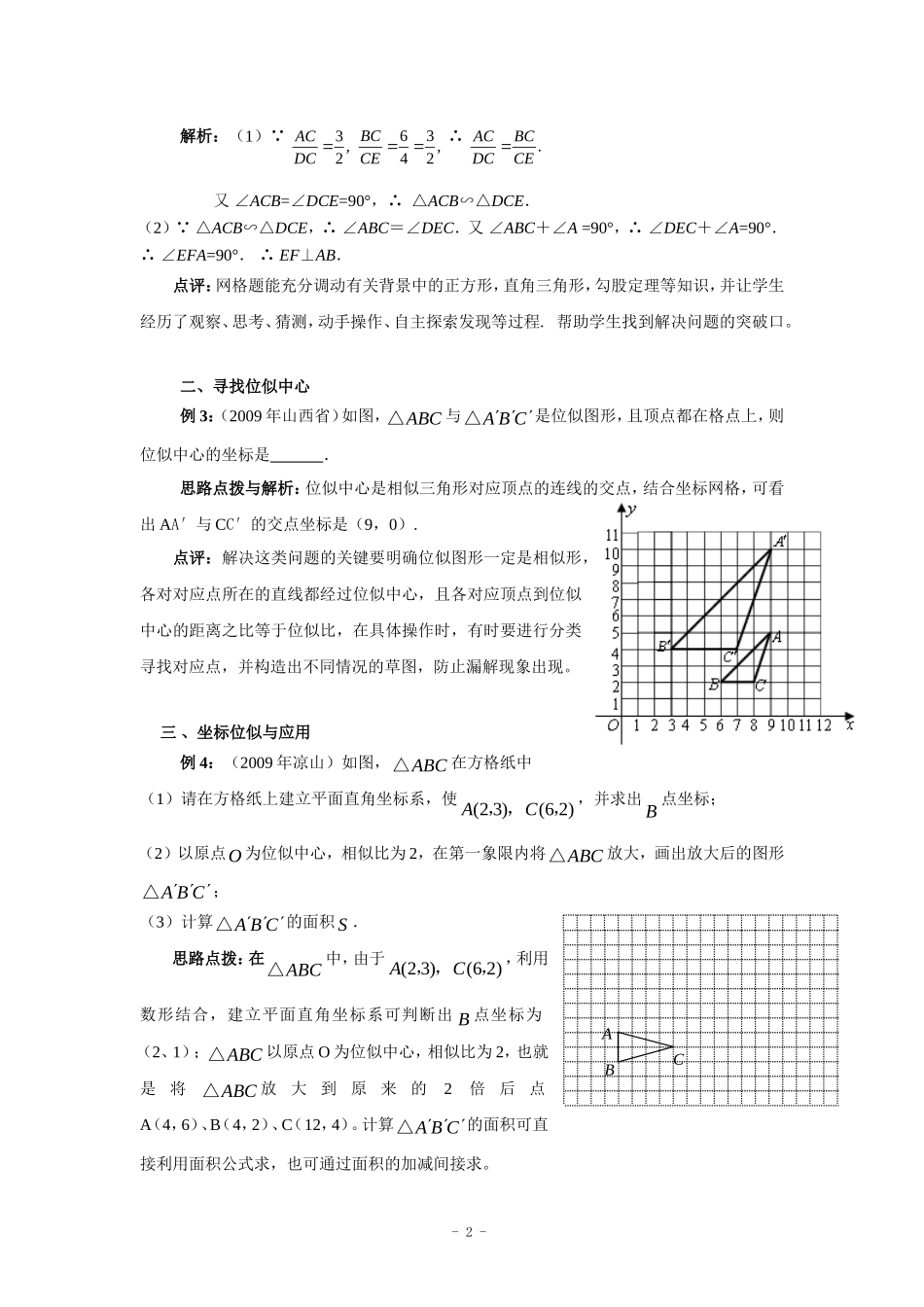
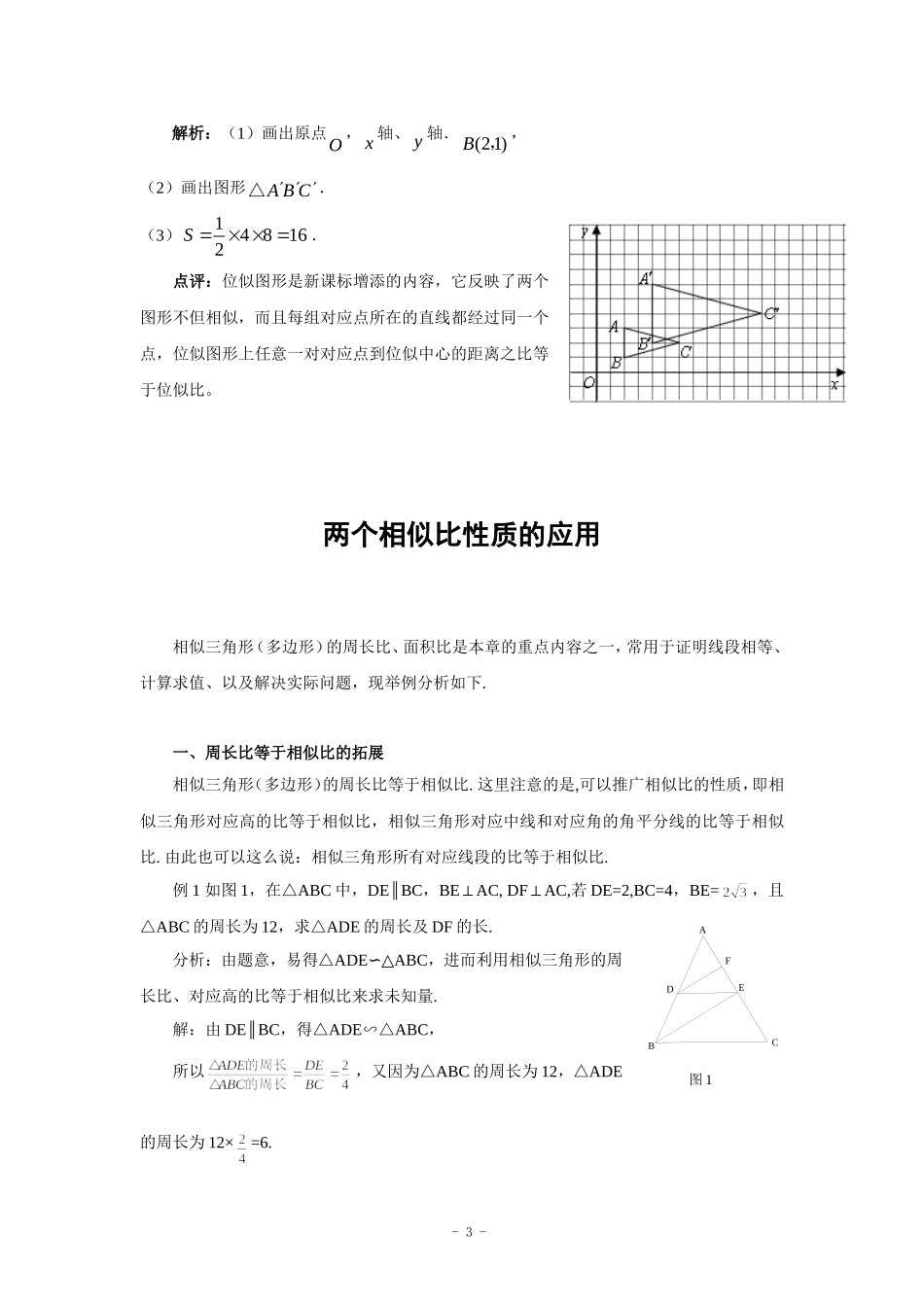
例谈相似在网格中的构建与应用在近几年的各类考试中,网格背景题深受命题者的关注与青睐。当网格作为背景时,相关格点之间便容易形成特殊的图形如正方形,直角三角形,勾股定理等知识,具有较强的直观性、操作性,较好地实现了数学基本知识、空间观念与多种数学思维能力的综合与运用,尤其是勾股定理、数形结合等思想方法的运用达到了极点。让我们从中感受到无穷的学习动力和学习乐趣,具有极大的学习创造性和挑战性。一、相似的判定与性质例1;(2009年新疆)如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与ABC△相似的是()思路点拨与解析:借助网格,由已知的ABC△可知,最大角∠ACB=135°,故排除选项B、C、D三项,故选A。点评:本题主要考查在网格背景中相似三角形的判定方法,解题的关键是准确把握ABC△在网格中的特有的本质;最大角∠ACB=135°。当然也可利用网格背景分别计算三角形的各边,利用三边对应成比例寻找两三角形相似。在此题中勾股定理、数形结合等思想的运用达到了极点。例2:(2009年甘肃庆阳)如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.(1)求证:△ACB∽△DCE;(2)求证:EF⊥AB思路点拨:解此题的关键是要处理三角形的边与角的相关信息:BC⊥AE,3162ACBC,2142DCEC,从而证出两三角形相似,要证EF⊥AB,只要证出∠DEC+∠A=90°,只要利用所证的两三角形相似知识即可证出。-1-A.解析:(1) 3,2ACDC63,42BCCE∴.ACBCDCCE又∠ACB=∠DCE=90°,∴△ACB∽△DCE.(2) △ACB∽△DCE,∴∠ABC=∠DEC.又∠ABC+∠A=90°,∴∠DEC+∠A=90°.∴∠EFA=90°.∴EF⊥AB.点评:网格题能充分调动有关背景中的正方形,直角三角形,勾股定理等知识,并让学生经历了观察、思考、猜测,动手操作、自主探索发现等过程.帮助学生找到解决问题的突破口。二、寻找位似中心例3:(2009年山西省)如图,ABC△与ABC△是位似图形,且顶点都在格点上,则位似中心的坐标是.思路点拨与解析:位似中心是相似三角形对应顶点的连线的交点,结合坐标网格,可看出AA′与CC′的交点坐标是(9,0).点评:解决这类问题的关键要明确位似图形一定是相似形,各对对应点所在的直线都经过位似中心,且各对应顶点到位似中心的距离之比等于位似比,在具体操作时,有时要进行分类寻找对应点,并构造出不同情况的草图,防止漏解现象出现。三、坐标位似与应用例4:(2009年凉山)如图,ABC△在方格纸中(1)请在方格纸上建立平面直角坐标系,使(23)(62)AC,,,,并求出B点坐标;(2)以原点O为位似中心,相似比为2,在第一象限内将ABC△放大,画出放大后的图形ABC△;(3)计算ABC△的面积S.思路点拨:在ABC△中,由于(23)(62)AC,,,,利用数形结合,建立平面直角坐标系可判断出B点坐标为(2、1);ABC△以原点O为位似中心,相似比为2,也就是将ABC△放大到原来的2倍后点A(4,6)、B(4,2)、C(12,4)。计算ABC△的面积可直接利用面积公式求,也可通过面积的加减间接求。-2-ABC解析:(1)画出原点O,x轴、y轴.(21)B,,(2)画出图形ABC△.(3)148162S.点评:位似图形是新课标增添的内容,它反映了两个图形不但相似,而且每组对应点所在的直线都经过同一个点,位似图形上任意一对对应点到位似中心的距离之比等于位似比。两个相似比性质的应用相似三角形(多边形)的周长比、面积比是本章的重点内容之一,常用于证明线段相等、计算求值、以及解决实际问题,现举例分析如下.一、周长比等于相似比的拓展相似三角形(多边形)的周长比等于相似比.这里注意的是,可以推广相似比的性质,即相似三角形对应高的比等于相似比,相似三角形对应中线和对应角的角平分线的比等于相似比.由此也可以这么说:相似三角形所有对应线段的比等于相似比.例1如图1,在△ABC中,DE∥BC,BE⊥AC,DF⊥AC,若DE=2,BC=4,BE=,且△ABC的周长为12,求△ADE的周长及DF的长.分析:由题意,易得△ADE∽△ABC,进而利用相似三角形的周长比、对应高的比等于相似...