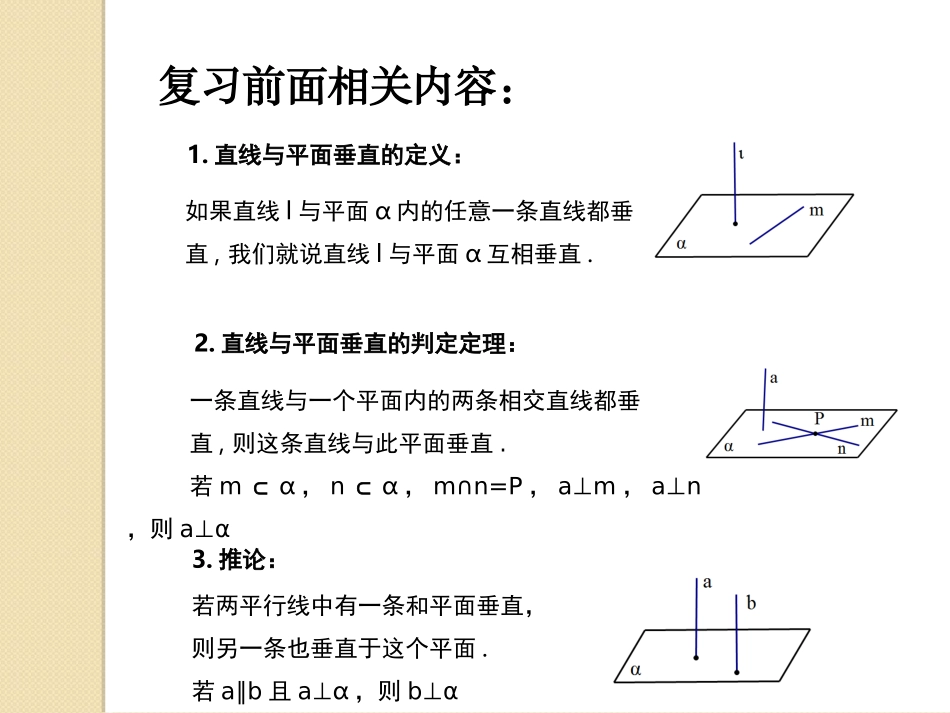
§2.3.3直线与平面垂直的性质教师:邓宏刚1.理解直线与平面垂直的性质定理,能用图形语言和符号语言表述这些定理,并能加以证明.2.能运用直线与平面垂直的性质定理证明一些空间位置关系的简单问题.教学目标:复习前面相关内容:1.直线与平面垂直的定义:如果直线l与平面α内的任意一条直线都垂直,我们就说直线l与平面α互相垂直.2.直线与平面垂直的判定定理:一条直线与一个平面内的两条相交直线都垂直,则这条直线与此平面垂直.若m⊂α,n⊂α,m∩n=P,a⊥m,a⊥n,则a⊥α3.推论:若两平行线中有一条和平面垂直,则另一条也垂直于这个平面.若a∥b且a⊥α,则b⊥α4.三垂线定理及逆定理:三垂线定理:平面内的一条直线和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。a⊂α,PO⊥α,若aOA⊥,则aPA⊥逆定理:平面内的一条直线和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。a⊂α,PO⊥α,若aPA⊥,则aOA⊥5.总要结论:①过一点有个平面和已知直线垂直.②过一点有条直线和已知平面垂直.且只有一且只有一1.直线与平面垂直的性质:(1)一直线垂直于一平面,则此直线和该平面内的任意直线都垂直(2)直线与平面垂直的性质定理①定理:垂直于同一个平面的两条直线平行②图像表示:③符号语言:。若a⊥α,b⊥α,则ab∥④作用:证明线线平行;构造平行线2.重要结论:①结论:与同一条直线垂直的两个平面平行②证明:③图像表示④符号语言:若lα⊥,且lβ⊥,则αβ∥3.运用例一:判断正误①如果一条直线垂直于一个平面内的无数条直线,那么这条直线和这个平面垂直;②过空间一点有且只有一条直线与已知平面垂直;③一条直线和一个平面不垂直,那么这条直线和平面内的所有直线都不垂直;④垂直于同一直线的两直线平行⑤垂直于同一平面的两条直线平行✘√✘√✘例二:如图,已知α∩β=AB,EC⊥平面α,C为垂足,ED⊥平面β,D为垂足.求证:CD⊥AB.证明:∵ECα,ABα,ECAB,⊥⊂∴⊥同理EDAB,⊥即ABEC,ABED,⊥⊥又EC∩ED=E,AB∴⊥面ECD,而CD⊂面ECD,ABCD.∴⊥例三:如图,已知正方体ABCD—A1B1C1D1中,EF与异面直线AC、A1D都垂直相交,求证:EF∥BD1.证明:连接AB1,B1C,BD,∵DD1⊥平面ABCD,AC⊂平面ABCD,∴DD1AC.⊥又∵ACBD,⊥∴AC⊥平面BDD1B1,ACBD∴⊥1.同理BD1B⊥1C,BD∴1⊥平面AB1C.∵EFA⊥1D,且A1DB∥1C,EFB∴⊥1C.又∵EFAC,⊥∴EF⊥平面AB1C,EFBD∴∥1.4.思考题:如图(左图)所示,等边三角形ABC边长为1,D,E分别是AB,AC边上的点,且AD=AE,F是BC上的中点,AF与DE交与点G。将△ABF沿AF折起,得到如图(右图)所示的三棱锥A-BCF,BC=√2/2,①求证DE∥平面BCF②求证CF⊥平面ABF5.作业课本P71:1,2题