1.1-探索勾股定理课件VIP免费

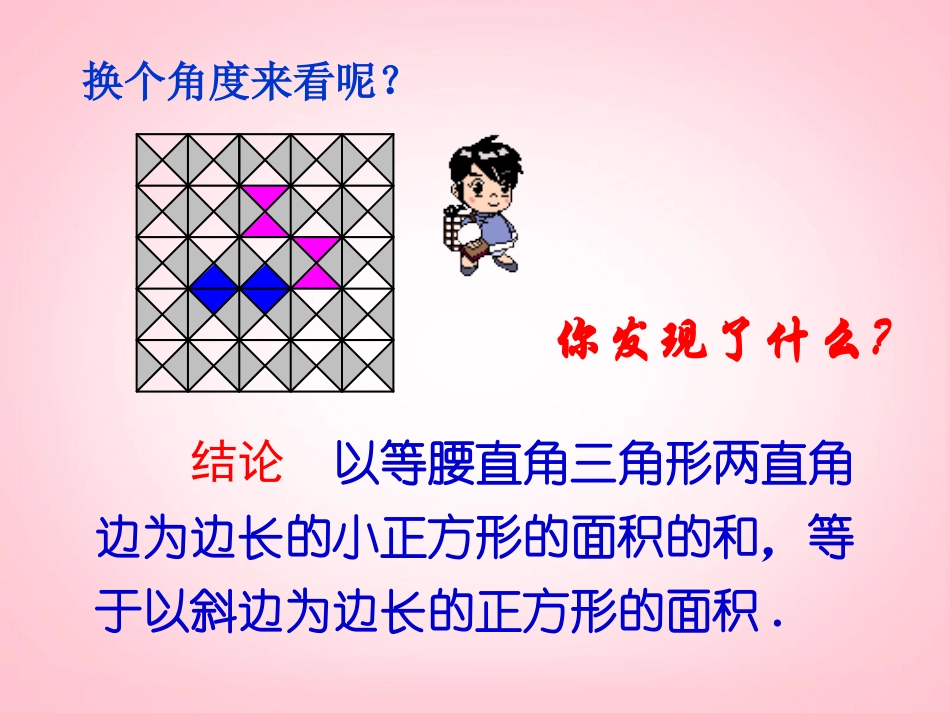
探索勾股定理探索勾股定理八年级数学（上册）八年级数学（上册）瓜州县第二中学杨学明探究活动一：观察下面地板砖示意图：探索发现勾股定理观察这三个正方形你发现图中三个正方形的面积之间存在什么关系吗？换个角度来看呢？结论以等腰直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.你发现了什么？ABCABC（图中每个小方格代表一个单位面积）图1-1图1-2（1）观察图1-1正方形A中含有个小方格，即A的面积是个单位面积。正方形B的面积是个单位面积。正方形C的面积是个单位面积。999你想知道老师是怎样得到上面的结果的吗？探究活动二：18ABCABC（图中每个小方格代表一个单位面积）图1-1图1-2cS正方形1433182把正方形C分割成四个直角边为整数的直角三角形（单位面积）ABCABC（图中每个小方格代表一个单位面积）图1-1图1-2cS正方形216218（单位面积）把看成边长为6的正方形面积的一半cS正方形ABCABC（图中每个小方格代表一个单位面积）图1-1图1-2（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？（3）你能发现图1-1、图1-2中三个正方形A，B，C的面积之间有什么关系吗？SA+SB=SC即：两条直角边上的正方形面积之和等于斜边上的正方形的面积A的面积B的面积C的面积图1-19918图1-2448ABC图1-3ABC图1-4（1）观察图1-3、图1-4，并填写下表：A的面积（单位面积）B的面积（单位面积）C的面积（单位面积）图1-3图1-4169254913你想知道老师是怎样得到上面的结果的吗？探究活动三：ABC图1-3ABC图1-4分割成四个直角边为整数的直角三角形和一个小正方形cS正方形25144312（面积单位）)(13132214面积单位正方形CSABC图1-3ABC图1-4（2）图1-3、图1-4中三个正方形A，B，C的面积之间有什么关系？SA+SB=SC即：两条直角边上的正方形面积之和等于斜边上的正方形的面积（1）你能用三角形的边长表示正方形的面积吗？（2）你能发现直角三角形三边长度之间存在什么关系吗？探究活动四：ABC图1-3ABC图1-4aabbcc2aAS正方形2bBS正方形2cCS正方形CBASSS正方形正方形正方形222cba勾股定理（gou-gutheorem)如果直角三角形两直角边分别为a、b,斜边为c，那么222abc即直角三角形两直角边的平方和等于斜边的平方。abc勾股弦在西方又称毕达哥拉斯定理耶！再见再见