锐角三角函数PPT刘林VIP免费

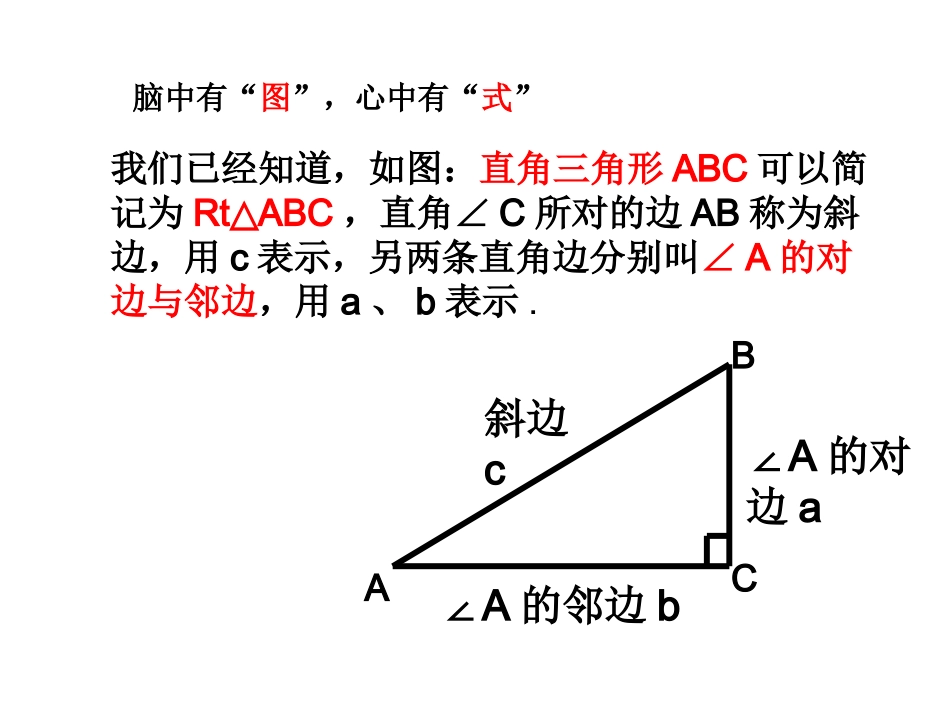
华师版九年级数学(上册)第二十四章24.3.1锐角三角函数新店中学刘林我们已经知道，如图：直角三角形ABC可以简记为RtABC△，直角∠C所对的边AB称为斜边，用c表示，另两条直角边分别叫∠A的对边与邻边，用a、b表示.∠A的对边a脑中有“图”，心中有“式”BAC∠A的邻边b斜边cab那么，RtABC△有哪些性质？c90BA角的性质：222cba边的性质：除了这些性质之外，那么边和角之间有没有联系呢？BACA1B1C1△ABCA∽△1B1C11111CAACCBBC当我们知道视线与水平线的夹角为34度时，能否直接求出旗杆的高度呢？•观察图中的RtAB△1C1、RtAB△2C2和RtAB△3C3，它们相似吗？RtAB△1C1RtAB∽△2C2RtAB∽△3C3可见，在RtABC△中，对于锐角A的每一个确定的值，其对边与邻边的比值是唯一确定的.B2C2AC2B3C3AC3所以＝__________=__________.B1C1AC1AC1C2C3B3B1B2对于锐角A的每一个确定的值，其对边与斜边、邻边与斜边、邻边与对边的比值也是唯一确定的吗？想一想AC1C2C3B3B1B2结论：由相似三角形的性质得，只要∠A不变，那么都有：BCAB111BCABACAB11ACABBCAC111BCAC===ABB1CC1即在直角三角形中，当锐角A取一定度数时，不管三角形的大小如何，∠A的对边与斜边的比是一个固定值，叫做∠A的正弦，记作sinA；邻边与斜边的比是一个固定值，叫做∠A的余弦，记作cosA；对边与邻边的比是一个固定值，叫做∠A的正切，记作tanA。在Rt△ABC中及时总结经验，要养成积累方法和经验的良好习惯！=ab的邻边的对边AAtanA=cotA=∠A的邻边∠A的对边=ab=acsinA=斜边的对边A=bccosA=斜边的邻边A在RtABC中对于锐角A的每一个确定的值，sinA、cosA、tanA、cotA都有唯一的确定的值与它对应，所以把锐角A的正弦、余弦、正切、余切叫做∠A的锐角三角函数。注意：1.1.我们研究的锐角三角函数都是在我们研究的锐角三角函数都是在直角三角形直角三角形中定义的中定义的..22..三角函数的实质是三角函数的实质是一个比值一个比值，且都大于，且都大于00，没有单位，，没有单位，而且这个比值只与锐角的大小有关与三角形边长无关而且这个比值只与锐角的大小有关与三角形边长无关..33..sinA、cosA、tanA、cotA都是表达符号,它们是一个整体,不能拆开来理解.4.sinA、cosA、tanA、cotA中∠A的角的记号“∠”习惯省略不写,但对于用三个大写字母和阿拉伯数字表示的角,角的记号“∠”不能省略.如sin1∠不能写成sin1.5.角相等,则其三角函数值相等；两锐角的三角函数值相等,则这两个锐角相等.ABC例1如图,在RtABC△中,∠C=90°AB=5,BC=3,求∠A,B∠的正弦,余弦和正切.观察以上计算结果,你发现了什么?若AC=5,BC=3呢?解：在RtABC△中,4352222BCABAC因此43tan54cos53sinAAA34tan53cos54sinBBB1tantansincoscossinBABABAtanA与cotA的关系：sinA与cosA的关系：tanA与sinA、cosA之间的关系：cotA与sinA、cosA之间的关系：sin2A+cos2A=1tanA·cotA=1sinAcosAtanA=cosAsinAcotA=利用直角三角形三边关系得到：00,cotA>0即锐角A的四个三角函数值都是正数。我来试一试：1、如图1，在Rt△MNP中，∠N＝90゜.∠P的对边是_______,∠P的邻边是___________;∠M的对边是________,∠M的邻边是___________;2、求出如图2所示的Rt△DEC(∠E＝90゜)中∠D的四个三角函数值(用字母表示).3、设Rt△ABC，∠C＝90゜∠A、∠B、∠C的对边分别为a、b、c，根据下列所给条件∠B的四个三角函数值：（1）a=3，b=4；（2）a=5，c=13.例2如图:在Rt△ABC中,∠B=900,AC=200,sinA=0.6.求:BC的长.200ACB┌解：在RtABC△中12060200sinsinAACBCACBCA知识回顾：•本节课我学会了：•1、•2、•……