【人教A版-选修1-1】2013年数学暑期备课《椭圆及其标准方程》课件(1)VIP免费

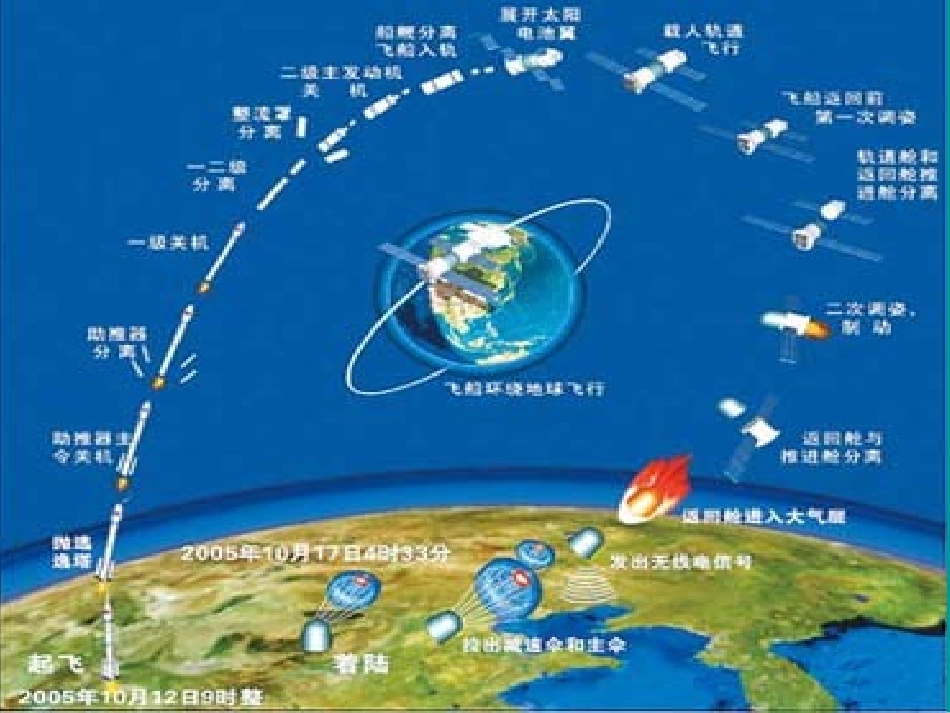
课题：椭圆及其标准方程（一）授课教师：北京市陈经纶中学黎宁——仙女座星系星系中的椭圆——“传说中的”飞碟求曲线方程的一般步骤：建系列式设点证明化简F2F1Oxy第一步建系、设点Oxy1F2F1F2Fx以两定点、所在直线为轴，线段y21FF的垂直平分线为轴，建立直角坐标系.cFF221)0(c设，、),c(F01)0,(2cF则),(yxM为椭圆上的任意一点，)22(ca又设a2的和等于、M1F2F与的距离MaMFMFMP221M椭圆上点的集合为aycxycx2)()(2222移项平方，得2222222)()(44)(ycxycxaaycx整理得222)(ycxacxa上式两边再平方，得2222222222422yacacxaxaxccxaa整理得)()(22222222caayaxcaaycxycx2)()(2222m,p,n成等差数列m+n=2p，a22)(ycx22)(ycx知，成等差数列，三个数成等差数列的表示方法“x-d,x,x+d”dada②①daycxdaycx2222设22②①adcx44，得：2222222axcacyx将③代入④式，得22222222caayaxca整理，得acxd，即③22②①22222xycad，得：④化标准②①daycxdaycx2222设22②①③22222dacyx，得：22②①adcx44，得：2222222axcacyx将④代入③式，得22222222caayaxca整理，得acxd，即④22222222caayaxca联想图形222222bayaxb222cab令，得12222byax22ba两边同时除以，得0ba012222babyax对照：Oxy②我们没有证明“以满足方程的解为坐标的点都在椭圆上”；③不同的建系方式，求出的椭圆方程是不同的．小结：x①此方程表示的椭圆的焦点在轴上；)0(12222babxayF1F2MxyO焦点在轴上的椭圆标准方程：y①椭圆的焦点在y轴,坐标为F1（0，-c）、F2（0，c）;②22abc两种形式的标准方程的比较：两种形式的标准方程的比较：012222babyax与222210yxabab椭圆的焦点在x轴上椭圆标准方程中x2项的分母较大；椭圆的焦点在y轴上椭圆标准方程中y2项的分母较大．例2小结思考题04，04，例求适合下列条件的椭圆的标准方程．①两个焦点的坐标分别是、椭圆上一点到两焦点距离的和等于10．小结例24c9222cab192522yx102a5a解：由题意可知∴，所以所求椭圆的标准方程为:小结①焦点坐标：（-4，0）、（4，0），椭圆上一点到两焦点距离的和等于10．20，②两个焦点的坐标分别是20，、2523，并且经过点．例求适合下列条件的椭圆的标准方程．小结解法222221yxab0ab102225232252322222a161022xyy因为椭圆的焦点在轴上，所以设它的标准方程为由椭圆的定义知：6222cab10a2c∴，又，∴所以所求椭圆的标准方程为：解：小结12222bxay0ba412325222222baba解:设所求的标准方程为依题意得61022ba161022xy解得:所以所求椭圆的标准方程为:．小结“”神舟六号运行轨道的方程.A2F“”如图，神舟六号载人飞船的运行轨道是以地心（地球的中心）为一个焦点的椭圆，已知它的近地点（离Bkm地面最近的点）距地面200，远地点（离地面最近．．B2F1FAkm的点）距地面约350，椭圆的另一个焦点是，且1FBA、2F、1F、在同一直线上，km地球半径约为6400，求思考题:km（精确到1，参考数据：）445500006674小结．．B2F1FAOxy求椭圆的方程km近地点距地面200，km地球半径约为6400，km（精确到1km远地点距地面350，解：由题意可知ac=6400+200ac=6400+350解得：a=6675，c=75222667575b445500002222166756674xy故为椭圆方程．参考数据：）445500006674归纳、小结：归纳、小结：1．椭圆的定义：平面内与两个定点2F1F、的距离的和的点的轨迹是椭圆．等于常数(大于)21FF12222byax0ba12222bxay0bax2．椭圆的标准方程焦点在轴上椭圆的标准方程为：...