1.3探索三角形全等的条件(5)VIP免费

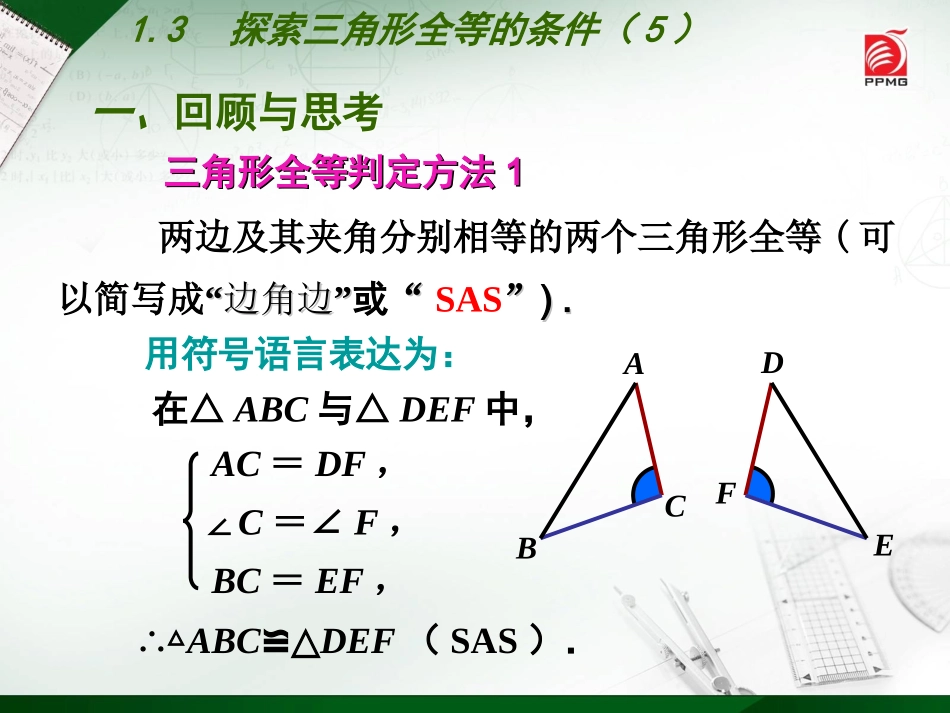
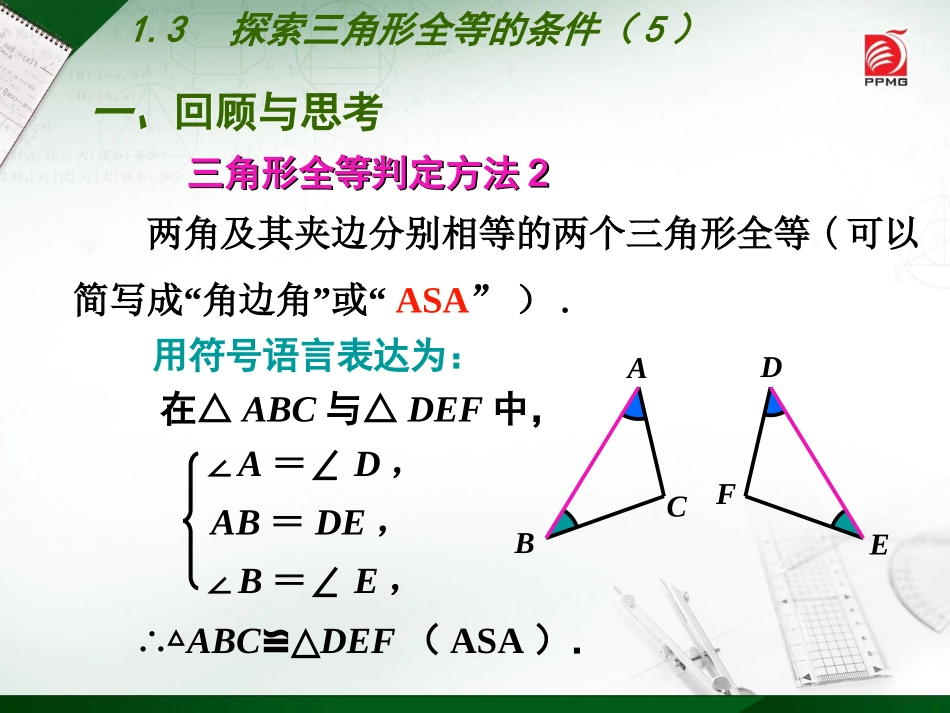
八年级(上册)初中数学1.3探索三角形全等的条件（5）三角形全等判定方法三角形全等判定方法11用符号语言表达为：在△ABC与△DEF中，∴△ABC≌△DEF（SAS）．两边及其夹角分别相等的两个三角形全等(可以简写成“”边角边“”边角边或““SAS””).).FEDCBAAC＝DF，∠C＝∠F，BC＝EF，一、回顾与思考一、回顾与思考1.3探索三角形全等的条件（5）两角及其夹边分别相等的两个三角形全等(可以简写成“角边角”或“ASA”）.FEDCBA三角形全等判定方法三角形全等判定方法22在△ABC与△DEF中，∴△ABC≌△DEF（ASA）．∠A＝∠D，AB＝DE，∠B＝∠E，用符号语言表达为：一、回顾与思考一、回顾与思考1.3探索三角形全等的条件（5）三角形全等判定方法3两角分别相等且其中一组等角的对边相等的两个三角形全等(可以简写成“角角边”或“AAS”）.用符号语言表达为：在△ABC与△DEF中，∴△ABC≌△DEF（AAS）．∠A＝∠D，∠B＝∠E，AC＝DF，CBAACBFEDFDE1.3探索三角形全等的条件（5）一、回顾与思考一、回顾与思考如图，已知AD平分∠BAC，要使△ABD≌△ACD，(1)根据“SAS”需添加条件；(2)根据“ASA”需添加条件；(3)根据“AAS”需添加条件．AB＝AC∠BDA＝∠CDA∠B＝∠C1.3探索三角形全等的条件（5）一、回顾与思考一、回顾与思考•下列语句：①面积相等的两个三角形全等；②面积不等的三角形不全等；③两个等边三角形一定是全等图形；④如果两个三角形全等，它们的形状和大小一定都相同；⑤边数相同的图形一定能互相重合。其中错误的说法有()•A.4个B.3个•C.2个D.1个错误的举一个反例。1．如图,∠A＝∠B，∠1＝∠2，EA＝EB，你能证明AC＝BD吗?二、分析与讨论二、分析与讨论证明:∵∠1＝∠2（已知），∴∠1＋∠BEC＝∠2＋∠BEC，∴∠AEC＝∠BED，在△EAC和△EBD中，∠A＝∠B（已知），EA＝EB（已知），∠AEC＝∠BED（已证），∴△EAC≌△EBD（ASA），∴AC＝BD．1.3探索三角形全等的条件（5）2．如图,点C、F在AD上,且AF＝DC,∠B＝∠E,∠A＝∠D，你能证明AB＝DE吗?证明:∵AF＝DC(已知)，∴AF－FC＝DC－FC，∴AC＝DF，在△ABC和△DEF中，∠B＝∠E(已知)，∠A＝∠D(已知)，AC＝DF(已证)，∴△ABC≌△DEF(AAS)，∴AB＝DE．二、分析与讨论二、分析与讨论1.3探索三角形全等的条件（5）1“．为了利用ASA”或“AAS”定理判定两个三角形全等，有时需要先把已知中的某个条件，转变为判定三角形全等的直接条件.三、归纳与总结三、归纳与总结2．证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到.1.3探索三角形全等的条件（5）四、理解与应用四、理解与应用例已知：如图，点A、B、C、D在一条直线上，EA∥FB，EC∥FD，EA＝FB.求证：AB＝CD．证明：∵EA∥FB，EC∥FD(已知)∴∠A＝∠FBD，∠ECA＝∠D，在△EAC和△FBD中，∠A＝∠FBD(已证)，∠ECA＝∠D(已证)，EA＝FB(已知)，∴△EAC≌△FBD(AAS)．∴AC＝BD，即AB＋BC＝CD＋BC，∴AB＝CD．1.3探索三角形全等的条件（5）上面的推理过程可以用符号“”简明地表述如下：四、理解与应用四、理解与应用1.3探索三角形全等的条件（5）EA∥FB∠A＝∠FBDEC∥FD∠ECA＝∠D△EAC≌△FBD△EAC≌△FBDEA＝FBAC＝BDAB＋BC＝CD＋BCAB＝CD五、巩固与练习五、巩固与练习已知：如图，AB＝AC，点D、E分别在AB、AC上，∠B＝∠C.求证：（1）DB＝EC.（2）△BOD≌△COE1.3探索三角形全等的条件（5）O变式一已知：∠1＝∠2，∠B＝∠C，AB＝AC.求证：AD＝AE，∠D＝∠E.12五、巩固与练习五、巩固与练习1.3探索三角形全等的条件（5）变式二已知：∠1＝∠2，∠B＝∠C，AB＝AC，D、A、E在一条直线上.求证：AD＝AE，∠D＝∠E.12五、巩固与练习五、巩固与练习1.3探索三角形全等的条件（5）1．如图，AC⊥AB，BD⊥AB，CE⊥DE，CE＝DE.求证：AC＋BD＝AB.六、拓展与提高六、拓展与提高1.3探索三角形全等的条件（5）2．如图，∠ABC＝90°，AB＝BC，D为AC上一点，分别过A、C作BD的垂线，垂足分别为E、F.求证：EF＋AE＝CF.六、拓展与提高六、拓展与提高1.3探索三角形全等的条件（5）七、课堂小结七、课堂小结通过这节课的学习与探索，你有哪些收获？1.3探索三角形全等的条件（5）