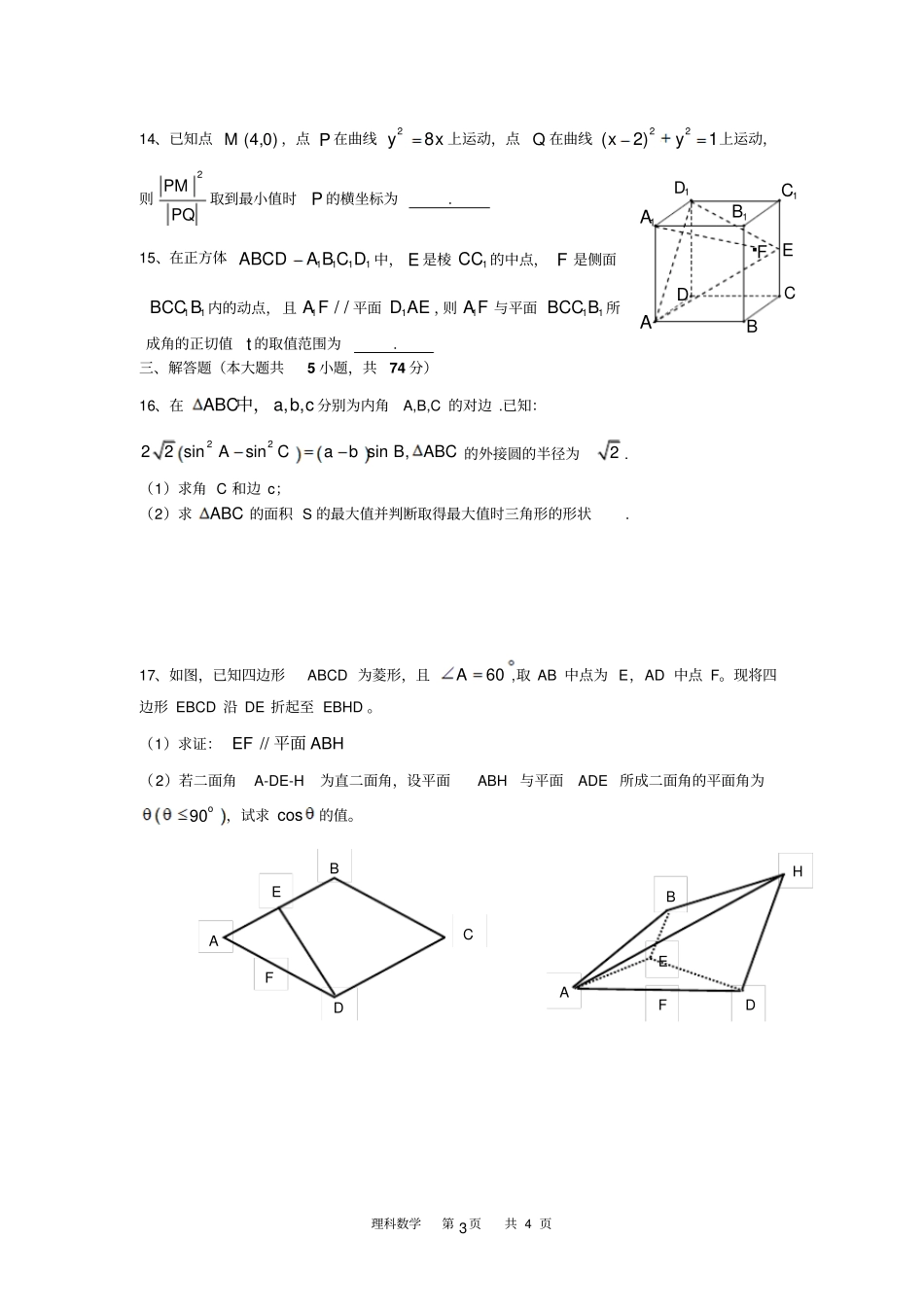
理科数学第页共4页12015年12月温州第八高级中学高三第三次月考数学试题(理科)(考试时间:150分钟,满分:150分命题人:吴银生审题人:于丛旭)参考公式:棱柱的体积公式VSh其中S表示棱柱的底面积,h表示棱柱的高棱锥的体积公式13VSh其中S表示棱锥的底面积,h表示棱锥的高球的表面积公式24SR棱台的体积公式112213VhSSSS球的体积公式343VR其中12,SS分别表示棱台的上底、下底面积,其中R表示球的半径h表示棱台的高选择题部分一、选择题(本大题共8题,每小题5分,共40分)1、设集合212,log2AxxBxx,则AB=()A.1,3B.1,4C.0,3D.,42、设na是等差数列,mnstN、、、,则“mnst”是“tsnmaaaa”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3、为了得到函数xxy3cos-3sin的图象,可将函数xy3sin2的图象()A.左平移4个单位B.向右平移4个单位C.向左平移12个单位D.向右平移12个单位4、已知ta2,tbln,tcsin,则使得cba成立的t可能取值为()A、0.5B、1C、2D、35、已知两条异面直线,以及空间给定一点,则()A.必存在经过该点的平面与两异面直线都垂直B.必存在经过该点的平面与两异面直线都平行C.必存在经过该点的直线与两异面直线都垂直D.必存在经过该点的直线与两异面直线都相交6、某公司招收男职员x名,女职员y名,xy和须满足约束条件247,239,211.xyxyx则理科数学第页共4页21010zxy的最大值是()A.80B.85C.90D.1007、定义域为[-2,1]的函数)(xf满足)(2)1(xfxf,且当]1,0[x时,xxxf2)(。若方程mxf)(有4个根,则m的取值范围为()A.]81,41[B.),(81-41-C.]161,81[D.),(161-81-8、已知椭圆C:12222byax,21FF,是椭圆的两个焦点,A为椭圆的右顶点,B为椭圆的上顶点。若在线段AB(不含端点)上存在不同的两个点21PP,,使得21AAPi和212AAP均为以21AA为斜边的直角三角形,则椭圆的离心率的取值范围为()A.)(22,21-5B.),(121-5C.)(21-5,0D.),(122非选择题部分二、填空题(本大题共7题,第9、10、11、12题每题6分,第13、14、15每空4分,共36分)9、已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为.表面积为.体积为.10、若等差数列{}na满足112a,465aa,则公差d______;24620aaaa______.11、若点)42(,P为抛物线22ypx上一点,则抛物线焦点坐标为;若双曲线22221(0,0)xyabab经过点P,且与抛物线共焦点,则双曲线的渐近线方程为.12、已知两个向量a,b的夹角为30°,3a,b为单位向量,btatc)1(,则c的最小值为.若cb=0,则t=.13、已知实数abc、、满足03cba则原点(0,0)O到直线0axbyc的距离的最大值为.侧(左)视图2理科数学第页共4页314、已知点)0,4(M,点P在曲线xy82上运动,点Q在曲线1)2(22yx上运动,则PQPM2取到最小值时P的横坐标为.15、在正方体1111ABCDABCD中,E是棱1CC的中点,F是侧面11BCCB内的动点,且1//AF平面1DAE,则1AF与平面11BCCB所成角的正切值t的取值范围为.三、解答题(本大题共5小题,共74分)16、在,,ABCabc中,分别为内角A,B,C的对边.已知:2222sinsinsin,ACabBABC的外接圆的半径为2.(1)求角C和边c;(2)求ABC的面积S的最大值并判断取得最大值时三角形的形状.17、如图,已知四边形ABCD为菱形,且60A,取AB中点为E,AD中点F。现将四边形EBCD沿DE折起至EBHD。(1)求证:ABHEF平面//(2)若二面角A-DE-H为直二面角,设平面ABH与平面ADE所成二面角的平面角为90o,试求cos的值。EFCBDAEBHDFAA1D1CDC1BB1AEF.理科数学第页共4页418、已知椭圆C两焦点坐标分别为1(3,0)F,2(3,0)F,且经过点1(3,)2P.(Ⅰ)求椭圆C的标准方程;(Ⅱ)若直线l经过左焦点1F,且与椭圆相交于A、B两点,判断1111BFAF是否为定值?若是求出此定值;若不是,说明理由。19、已知函数2()()xbfxbx为常数.(Ⅰ)当(1)(4)ff,函数()()Fxfxk有且仅有一个零点0x,且00x时,求k的值;(Ⅱ)若0b,用定义证明函数()yfx在区间),0(上为单调递增函数.(Ⅱ)若0b,当]3,1[x时不等式2)(xf恒成立,求b的取值范围.20、已知数列{}na、{}nb中,对任何正整数n都有:11213212122nnnnnnabababababn.(1)若数列{}na是首项和公差都是1的等差数...