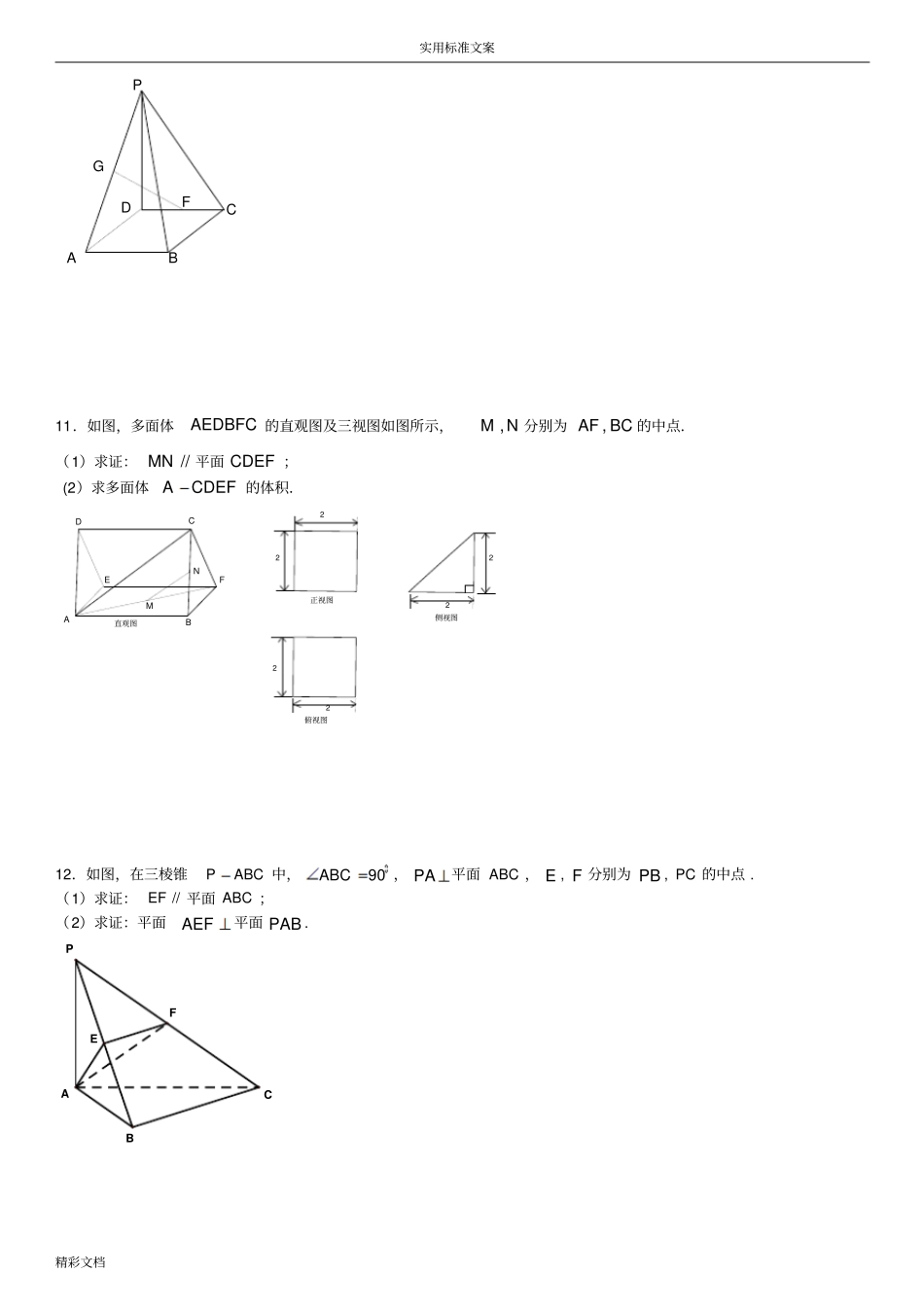
实用标准文案精彩文档立体几何1.用斜二测画法画出长为6,宽为4的矩形水平放置的直观图,则该直观图面积为()A.12B.24C.62D.1222.设,mn是不同的直线,,是不同的平面,下列命题中正确的是()A.若//,,mnmn,则B.若//,,mnmn,则//C.若//,,//mnmn,则⊥D.若//,,//mnmn,则//3.如图,棱长为1的正方体1111DCBAABCD中,P为线段BA1上的动点,则下列结论错误..的是A.PDDC11B.平面PAD11平面APA1C.1APD的最大值为090D.1PDAP的最小值为224.一个几何体的三视图如图所示(单位:m),则该几何体的体积为______m3.5.若某几何体的三视图如图所示,则此几何体的体积等于.6.如图是一个几何体的三视图,则该几何体的体积是____________实用标准文案精彩文档7.如图,一个盛满水的三棱锥容器,不久发现三条侧棱上各有一个小洞FED,,,且知1:2:::FSCFEBSEDASD,若仍用这个容器盛水,则最多可盛水的体积是原来的.8.如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=12PD.(1)证明:PQ⊥平面DCQ;(2)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.[来9.如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED面ABCD,3BAD.(1)求证://BCFAED平面平面.(2)若,BFBDaABDEF求四棱锥的体积。10.在四棱锥ABCDP中,底面ABCD为矩形,ABCDPD底面,1AB,2BC,3PD,FG、分别为CDAP、的中点.(1)求证:PCAD;(2)求证://FG平面BCP;SFCBADE实用标准文案精彩文档FGPDCBA11.如图,多面体AEDBFC的直观图及三视图如图所示,NM,分别为BCAF,的中点.(1)求证://MN平面CDEF;(2)求多面体CDEFA的体积.NMFEDCBA直观图俯视图正视图侧视图22222212.如图,在三棱锥PABC中,90ABC,PA平面ABC,E,F分别为PB,PC的中点.(1)求证://EF平面ABC;(2)求证:平面AEF平面PAB.FEACPB实用标准文案精彩文档13.如图,在三棱锥P—ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.求证:(1)直线PA∥平面DFE;(2)平面BDE⊥平面ABC.14.如图.直三棱柱ABC—A1B1C1中,A1B1=A1C1,点D、E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1(2)直线A1F∥平面ADE.BA1C1ECDAB1F实用标准文案精彩文档参考答案1.C【解析】试题分析:斜二测法:要求长边,宽减半,直角变为045角,则面积为:2645sin260.考点:直观图与立体图的大小关系.2.C【解析】试题分析:此题只要举出反例即可,A,B中由nmn,可得//n,则,可以为任意角度的两平面,A,B均错误.C,D中由nmn//,可得m,则有//,故C正确,D错误.考点:线,面位置关系.3.C【解析】试题分析:1DC面11BCDA,∴A正确;11AD面11AABB,∴B正确;当2201PA时,1APD为钝角,∴C错;将面BAA1与面11AABB沿BA1展成平面图形,线段DA1即为1PDAP的最小值,解三角形易得DA1=22,∴D正确.故选C.考点:线线垂直、线面垂直、面面垂直.4.4【解析】试题分析:已知三视图对应的几何体的直观图,如图所示:,所以其体积为:4211112V,故应填入:4.考点:三视图.5.24【解析】试题分析:由三视图可知,原几何体是一个三棱柱被截去了一个小三棱锥得到的,如图111345(34)324232V.考点:三视图.【答案】12【解析】实用标准文案精彩文档试题分析:该几何体是一个直三棱柱,底面是等腰直角三角形体积为12262V=12考点:三视图,几何体的体积.7.2723【解析】试题分析:过DE作截面平行于平面ABC,可得截面下体积为原体积的27193213)(,若过点F,作截面平行于平面SAB,可得截面上的体积为原体积的278323)(,若C为最低点,以平面DEF为水平上面,则体积为原体积的27233132321,此时体积最大.考点:体积相似计算.8.(1)祥见解析;(2)1.【解析】试题分析:(1)要证直线与平面垂直,只须证明直线与平面内的两条相交直线垂直即可,注意到QA⊥平面ABCD,所以有平面PDAQ⊥平面ABCD,且交线为AD,又因为四边形ABCD为正方形,由面面垂直的性质可得DC⊥平面PDAQ,从而有PQ⊥DC,又因为PD∥QA,且QA=AB=12PD,所以四边形PDAQ为直角梯形,利用勾股定理的逆定理可证PQ⊥QD;从而可证PQ⊥平面DCQ;(2)设AB=a,则由(1)及已知条件可用含a的式子表示...