1.3三角函数的诱导公式课件VIP免费

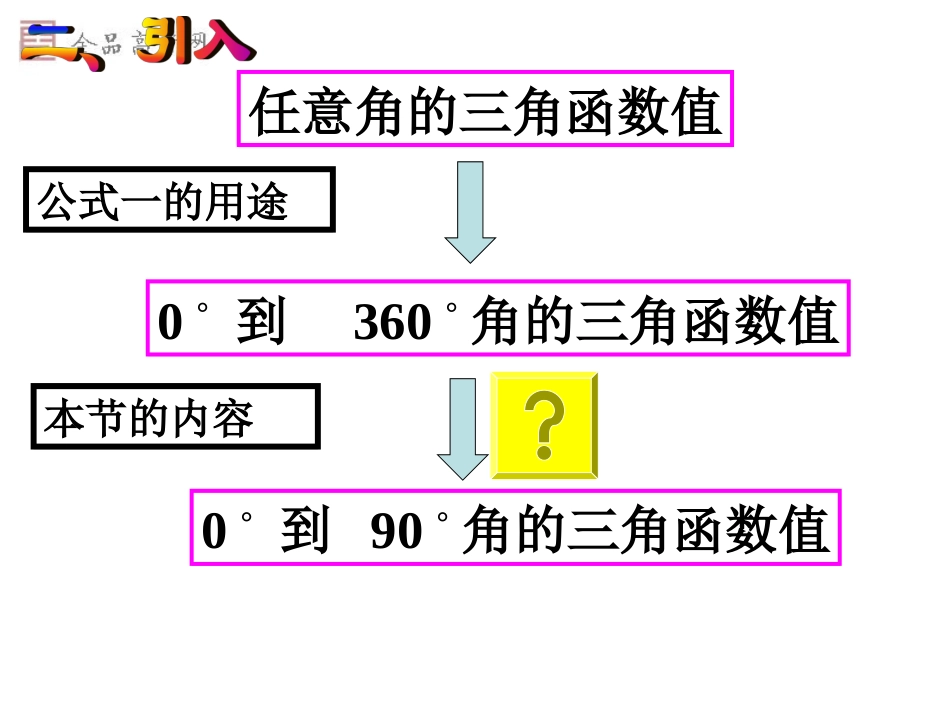
1.3三角函数的诱导公式公式一sin(α+k·360°)=sinαcos(α+k·360°)=cosαtan(α+k·360°)=tanα其中kZ∈公式一的用途任意角的三角函数值0°到360°角的三角函数值0°到90°角的三角函数值本节的内容给定一个角α(1)角π+α终边与角α的终边有什么关系?它们的三角函数之间有什么关系?探究+αyαxOP(x,y)πP(-x,-y)公式二sin(π+α)=－sinαcos(π+α)=－cosαtan(π+α)=tanα(2)角－α的终边与角α的终边有什么关系?它们的三角函数之间有什么关系?sin(－α)=－sinαcos(－α)=cosαtan(－α)=－tanα公式三yαxOP(x,y)-αP(x,-y)练习将下列三角函数转化为锐角三角函数,并填在题中横线上131cos______;2sin1______;93sin______;4cos706______.54cos9sin1sin5cos7016P27练习1(2)角π-α的终边与角α的终边有什么关系?它们的三角函数之间有什么关系?yαxOP(x,y)P(-x,y)απ-αsin(π-α)=sinαcos(π-α)=－cosαtan(π-α)=－tanαsin(π-α)=sinαcos(π-α)=－cosαtan(π-α)=－tanα公式四公式二sin(π+α)=－sinαcos(π+α)=－cosαtan(π+α)=tanαsin(π+α)=－sinαcos(π+α)=－cosαtan(π+α)=tanαsin(－α)=－sinαcos(－α)=cosαtan(－α)=－tanαsin(－α)=－sinαcos(－α)=cosαtan(－α)=－tanα公式三sin(π-α)=sinαcos(π-α)=－cosαtan(π-α)=－tanαsin(π-α)=sinαcos(π-α)=－cosαtan(π-α)=－tanα公式四α+k·2π(kZ),∈－α,π±α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.例1.利用公式求下列三角函数值:11161cos225;2sin;3sin;4cos2040.3321cos225cos18045cos4521132sinsin4sin3332161633sinsinsin5sin333324cos2040cos2040cos63601201cos1202利用公式一～四把任意角的三角函数转化为锐角函数,一般可按下面步骤进行:任意负角的三角函数任意正角的三角函数用公式三或一锐角三角函数用公式二或四0～2π的角的三角函数用公式一练习利用公式求下列三角函数值:1cos42072sin63sin1300794cos61cos60cos60251sinsin66253coscos6626428.040sin140sinP27练习2例2化简cos180sin360.sin180cos180cossin=1sincos原式:sin180解sin--180sin180sinsincos180cos180cos180cos练习31sin180cossin1802sincos2tan化简21=sincossinsincos原式342=sincostansin原式P27练习3练习反馈（1）已知，求的值．21cos9tan（2）已知，求的值．336cos65cossin(π+α)=－sinαcos(π+α)=－cosαtan(π+α)=tanαsin(π+α)=－sinαcos(π+α)=－cosαtan(π+α)=tanαsin(－α)=－sinαcos(－α)=cosαtan(－α)=－tanαsin(－α)=－sinαcos(－α)=cosαtan(－α)=－tanαsin(π-α)=sinαcos(π-α)=－cosαtan(π-α)=－tanαsin(π-α)=sinαcos(π-α)=－cosαtan(π-α)=－tanα小结三角函数的诱导公式作业课本习题1.3B组1