平行线综合复习.30)VIP免费

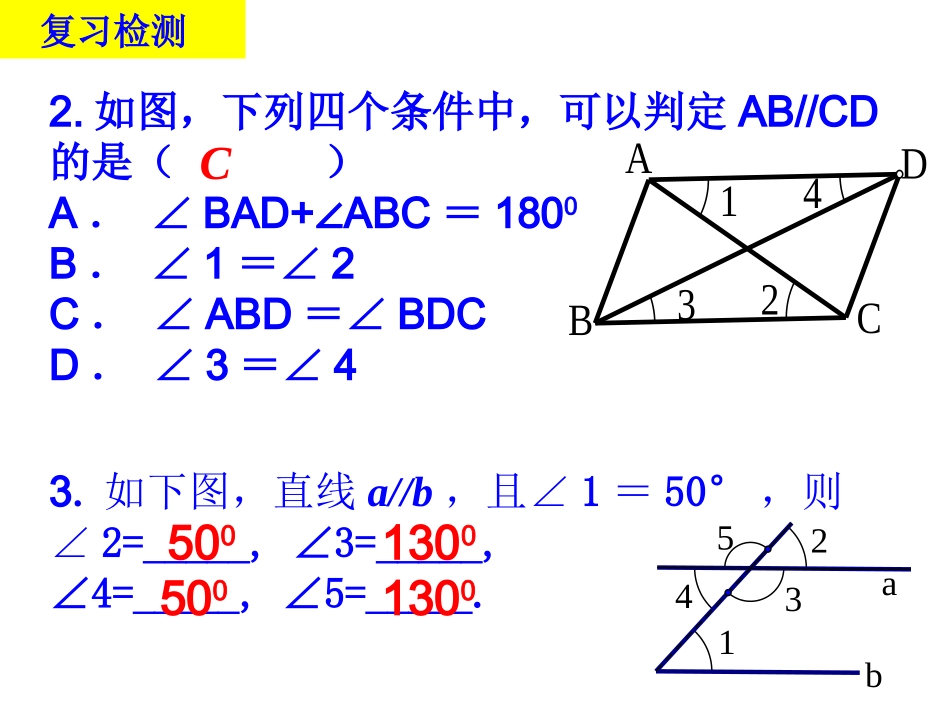
平行线的判定与性质综合运用(1)定义：在同一平面内,若直线a、b不相交，则a与b_____________。(2)i.若a//c,b//c,则a//bii.同一平面内，若a⊥b,a⊥c,则b//cabC平行复习平行（a//b）2.如图，下列四个条件中，可以判定AB//CD的是（）A．∠BAD+ABC∠＝1800B．∠1＝∠2C．∠ABD＝∠BDCD．∠3＝∠44321DCBA复习检测3.如下图，直线a//b，且∠1＝50°，则∠2=_____,∠3=_____,∠4=_____,∠5=_____.54321baC50013005001300已知∠1＝135°，∠2=45°，∠3=120°，则∠4=______。4231DBCA1200复习检测二．综合运用例1.已知：如图，AB//CD,BE、CF分别平分∠ABC和∠BCD。求证：__________________211______212CDAB//BCDABCBCDABC2121证明：∵BE、CF平分∠ABC和∠BCD（已知）∴,______________;()()∴()∴,即∠1=∠2.()∵∴BE//CF（）ABCBCD角平分线定义已知两直线平行，内错角相等内错角相等，两直线平行等式性质BE//CF二．综合运用例2：（1）已知：∠1＝∠2，∠A＝∠C，求证：AE//FCNM21FDECBA二．综合运用例2：（1）已知：∠1＝∠2，∠A＝∠C，求证：AE//FC（2）已知：ABEF⊥，CDEF⊥，∠A＝∠C，请问∠E＝∠F吗？试说明理由.NM21FDECBA三．提高例3：已知ABCD,AMP=150°,PND=60°∥∠∠，那么MPPN⊥吗？NMPDCBAKE三．提高例3：已知ABCD,AMP=150°,PND=60°∥∠∠，那么MPPN⊥吗？NMPDCBAKE解：MP⊥PN，理由如下：过点P作直线EK//AB，∴∠AMP+MPE=180°∠∵∠AMP=150°∴∠MPE=30°又∵ABCD,EK//AB∥∴EK//CD∴∠EPN=PND∠∵∠PND=60°∴∠EPN=60°∴∠MPN=MPE+EPN∠∠=60°+30°=90°即MPPN⊥三．提高例3：(1)如图1，当∠B与∠D满足________________的条件时，可以判断AB//CD;图1CDBA(3)如图2，当∠ABE、∠BED、∠CDE满足什么条件时，可以判断AB//CD？为什么？∠B+D=180∠0图2EABDC(2)如图3，当∠ABE、∠BED、∠CDE满足什么条件时，可以判断AB//CD？为什么？图3EABDCKEKE∠ABE+BED+CDE=360∠∠0∠ABE+CDE=BED∠∠同位角相等内错角相等同旁内角互补两直线平行同位角相等内错角相等同旁内角互补定义法传递法三．提高三．提高FABCDE变式：如图，已知AB//EF，∠B=360，∠E=1200，求∠D-∠C的大小。