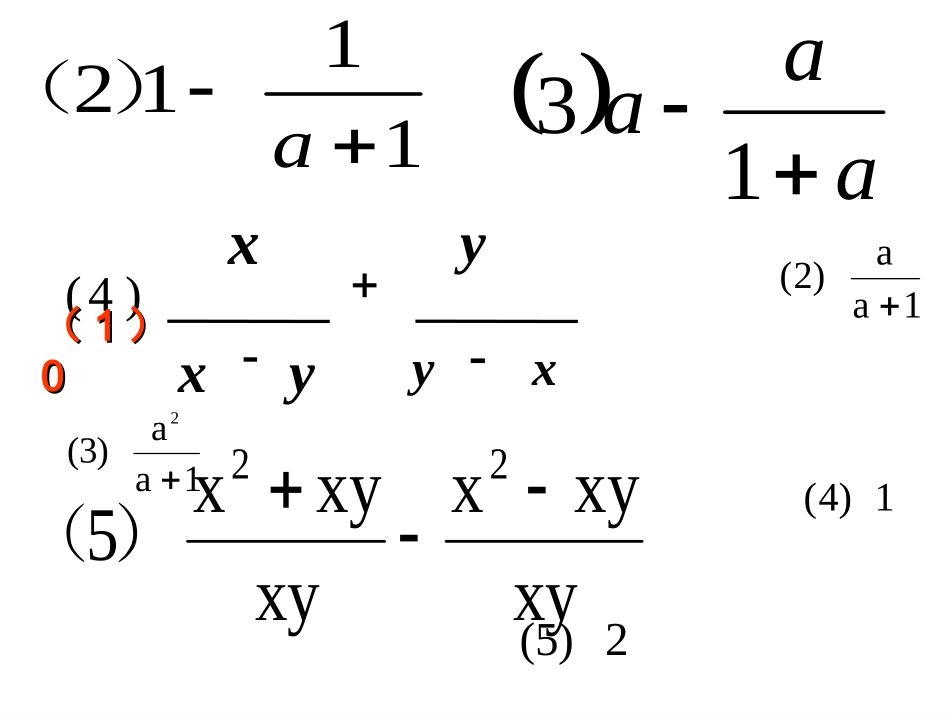g16.2.2(2)分式的加减2VIP免费

1112a）（xyxyxxyxyx522）（xyxyyx)4(aaa13（（11））001aa)2(1aa)3(21)4(2)5(计算：计算：4x4x2xx2x3322再来试试1124744312xxxyxyxyyxyxx2)1(1x1)2()2x(x3x)3(计算:4122bbababa先乘方；再乘除；最后加减；先乘方；再乘除；最后加减；有括号先做括号内．有括号先做括号内．分式的混合运算顺序：解：4122bbabababbababa41422)()(4)(44)(4222222babbaabababababa2222244444()()aaababababbababb1、2、xyyxxyyx22222211111212xxxxxx计算：试一试423y8x4xy)1(1x2x4x4)2(221111)1(2xxxxxxxxxxx4)44122)(2(22nmmnmnmm2121)3(再来试试1x)1(2)2x(1)2(1)3(1.2.3.4.1.2.3.4.aaaaaaaaa2444122222)225(423xxxxxxxxxxxx42442221a1a1a1a1a2aa8a42）（）（5.6.5.6.xxxxxx24222122412232aaaa2x1.1)6a)(2a(6a15.2xyxyxxyxyxx32327、1.解法一：1.解法一：aaaaaaaa42)2()1(4222aaaaaa4)2()2(4221aaaaaaaaaa24441222221.解法二：1.解法二：aaaaaaaaaaaa424414222222221aaaaaaaaaa2444122222aaaaaa42142=……2.解：2)2)(2(5423xxxxx292423xxxx)3(21x)225(423xxxxxxxxx)2)(2(2121xxxxxxxx)2)(2()2(1)2)(2()2(1xxxx22x43.解：xxxxxxxx42442224.解：)1)(1(4)1)(2()2(4aaaaaaaaaaaa4)1)(1()1(41a111112842aaaaaaaa）（）（仔细观察题目的结构特点，灵活运用运算律，适当运用计算技巧，可简化运算，提高速度，优化解题。分式的混合运算：关键是要正确的使用相应的运算法则和运算顺序；正确的使用运算律，尽量简化运算过程；结果必须化为最简分式。混合运算的特点：是整式运算、因式分解、分式运算的综合运用，综合性强。xyxyxxyxyxx3232例2.计算：1.解：原式解：原式yxxyxxyxyxx)(3232yxx2yxx2巧用分配律yxxxx131232babababa11)(1)(122把和看成整体，题目的实质是平方差公式的应用。ba1ba1例3.计算：巧用公式解：babababababa111111baba11babababa11)(1)(122222baa繁分式的化简：1.把繁分式转化成分子除以分母的形式，利用除法法则化简；2.利用分式的基本性质化简。