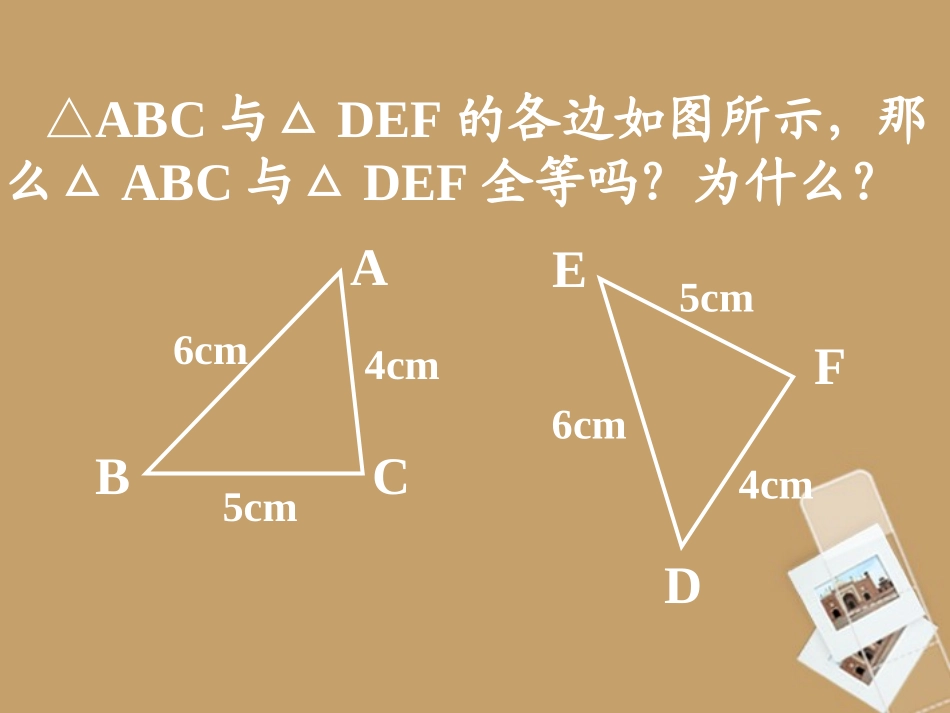
三角形全等的条件(1)三角形全等的条件(1)探究请同学们画一个三边长分别为4cm、5cm、6cm的三角形。Ⅰ.画线段AB=4cm;Ⅱ.分别以点A、B为圆心,5cm、6cm为半径画弧,两弧交于点C;Ⅲ.连结AC、BC。△ABC与△DEF的各边如图所示,那么△ABC与△DEF全等吗?为什么?ABCFE4cm5cm6cm4cm5cm6cmD新授如图,△ABC与△DEF中,AB=DE,AC=DF,BC=EF。ABCDEF两个三角形会全等吗?归纳三角形全等的条件1:三边对应相等的两个三角形全等。ABCDEF可以简写成:“边边边”或“SSS”将三根木条钉成一个三角形木架,这个三角形的形状、大小会改变吗?为什么?范例例1.如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架。求证:△ABDACD≌△。ABCD公共边隐含条件:已知:如图,AB=CD,BC=DA。求证:△ABCCDA≌△。ABCDAB∥CDBC∥DA公共边隐含条件:通过全等得角相等从而得平行方法:巩固已知:如图,AB=CD,BC=DA。求证:∠B=∠D。公共边隐含条件:添加辅助线构建全等方法:ABCD巩固如图,已知BD=CD,要根据“SSS”判定△ABDACD≌△,则还需添加的条件是。DABC公共边隐含条件:巩固工人师傅为了使电线杆AO垂直于地面BC,拉了两根钢丝AB、AC,并量得AB=AC,OB=OC,就断定电线杆AO一定与地面BC垂直,为什么?ABCO通过全等得角相等方法:巩固如图,AD=BC,要根据“SSS”判定△ABDBAC≌△,则还需添加的条件是()AOD=OCBOA=OBCAB=BADDB=CAOABCD公共边隐含条件:范例例2.已知:如图,AB=CD,BE=DF,AF=CE。求证:ABCD∥。ABCDCEF通过全等得角相等方法:部分共边隐含条件:巩固9.已知:如图,AB=CD,BE=DF,AF=CE。求证:BE∥DF。ABCDCEF部分共边隐含条件:巩固如图,AB=CD,AD=BC,则下列结论:①△ABCCDB;ABC≌△②△≌△CDA;ABD=CDB;BAD③△△④△=DCB.△正确的个数是()A1个B2个C3个D4个OABCD小结2、隐含条件的找法1、三角形全等的条件1:3、三角形全等的条件1的应用:通过证明三角形全等,从而证明相关的边相等或角相等公共边或部分共边SSS作业1.已知:如图,AB=AD,AC=AE,BC=DE,∠EAC=30°。求证:求∠DAB的大小。ABCDE作业2.已知:如图,AD=BC,CD=AB,求证:(1)DAC=BCA;∠∠(2)ACD=BAC.∠∠ABCDFE作业3.已知:如图,AB=CD,BC=DA。求证:AB∥CD。ABCD