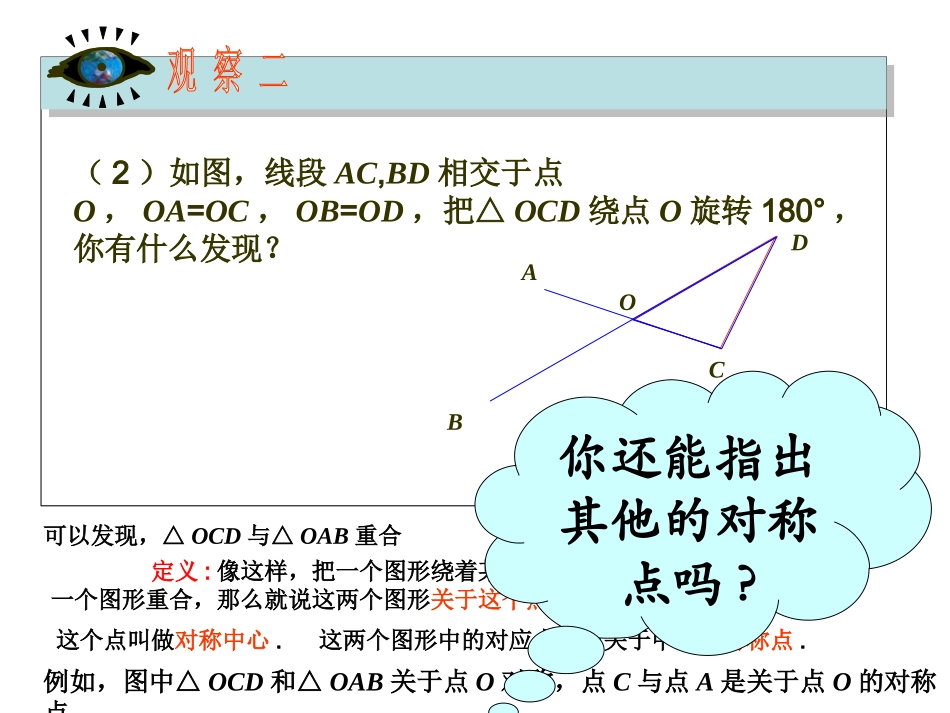
(1)如图,把其中一个图案绕点O旋转180°,你有什么发现?两个图案能够完全重合在一起例如,图中△OCD和△OAB关于点O对称,点C与点A是关于点O的对称点.(2)如图,线段AC,BD相交于点O,OA=OC,OB=OD,把△OCD绕点O旋转180°,你有什么发现?ABOCD可以发现,△OCD与△OAB重合定义:像这样,把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.你还能指出其他的对称点吗?畅所欲言:你在生活中见到过中心对称的应用吗?扩展资料中心对称在生活中的应用美在数学中1、广告商标中心对称应用于广告商标的设计制作,往往能以简单的色彩、线条,勾画出生动、富于创意和内涵的作品。因而只要你细心观察,就不难发现,原来中心对称就在我们身边!瞧,下边的图形你见过吗?、、2、工农业生产旋转的物体必须具有稳定性,而中心对称的设计恰恰满足了旋转物体的这一需求。因而在工农业生产制作转动工具时,都不可避免地考虑应用中心对称的设计,小的如日常生活中单车、闹钟内的齿轮,电风扇的扇叶;大的如推动飞机、轮船的轮桨,风力发电用的风车等等。另外,在日常使用的一些生活工艺品(如:地毯、挂毯),也不难发现中心对称的影子!ACBACBACBADEADE观察:两个图形关系如何?C.A.E三点的位置关系怎样?线段AC.AE的大小关系呢?如图,旋转三角板,画关于点O对称的两个三角形:第一步,画出△ABC;第二步,以三角板的一个顶点O为中心,把三角板旋转180°,画出△A′B′C′;第三步,移开三角板.这样画出的△ABC与△A′B′C′关于点O对称。分别连接对称点AA′、BB′、CC′.点O在线段AA′上吗?如果在,在什么位置?△ABC与△A′B′C′有什么关系?探究CABCABC′A′B′O(1)点A′是点A绕点O旋转180°后得到的,即线段OA绕点O旋转180°得到线段OA′,所以点O在线段AA′上,且OA=OA′,即点O是线段AA′的中点.CABC′A′B′O我们可以发现:(1)点O是线段AA′的中点;(2)△ABC≌△A′B′C′,上述发现可以证明.同样地,点O也是线段BB′和CC′的中点.∴△ABC≌△A′B′C′CABC′A′B′(2)在△AOB与△A′O′B′中,OA=OA′,OB=OB′,∠AOB=∠A′OB′,∴AB=A′B′.同理BC=B′C′,AC=A′C′.O∴△AOB≌△A′OB′(1)中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(2)中心对称的两个图形是全等图形.反过来,如果两个图形的对应点所连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.归纳:性质下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?A’B’C’ABCO(1)OA=OA′(1)OA=OA′、、OB=OB′OB=OB′、、OC=OC′OC=OC′(2)(2)△△ABCA≌△ABCA≌△′B′C′′B′C′深入理解你用什么方法识别两个图形是否关于某点成中心对称?A'CC'ABB'方法1:将其中一个图形绕某一点旋转180度,如果能够与另一个完全重合,那么它们关于这一点成中心对称。方法2:如果两个图形的对应点所连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.想一想中心对称与轴对称有什么区别?又有什么联系?轴对称中心对称有一条对称轴---直线有一个对称中心---点图形沿对称轴对折(翻折1800)后重合图形绕对称中心旋转1800后重合对称点的连线被对称轴垂直平分对称点的连线经过对称中心,且被对称中心平分关于中心对称的描述不正确的是()A.把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形对称;B.关于中心对称的两个图形是全等的;C.关于中心对称的两个图形,对称点的连线必过对称中心;D.如果两个图形关于点O对称,点A与A′是对称点,那么OA=OA′.联系:都是一个图形和另一个图形重合。练一练A小游戏:找朋友游戏规则:每位同学都作为平面内的一个点,挑选三位同学参加游戏,甲同学作为对称中心,大家一起找乙的朋友丙。如果丙同学能在大家发现之前站起来,丙就是游戏的胜利者,大家给予鼓掌奖励;反之,作为游戏的失败者,就要为大家唱一句最拿手的歌。※课外练习:预习新课