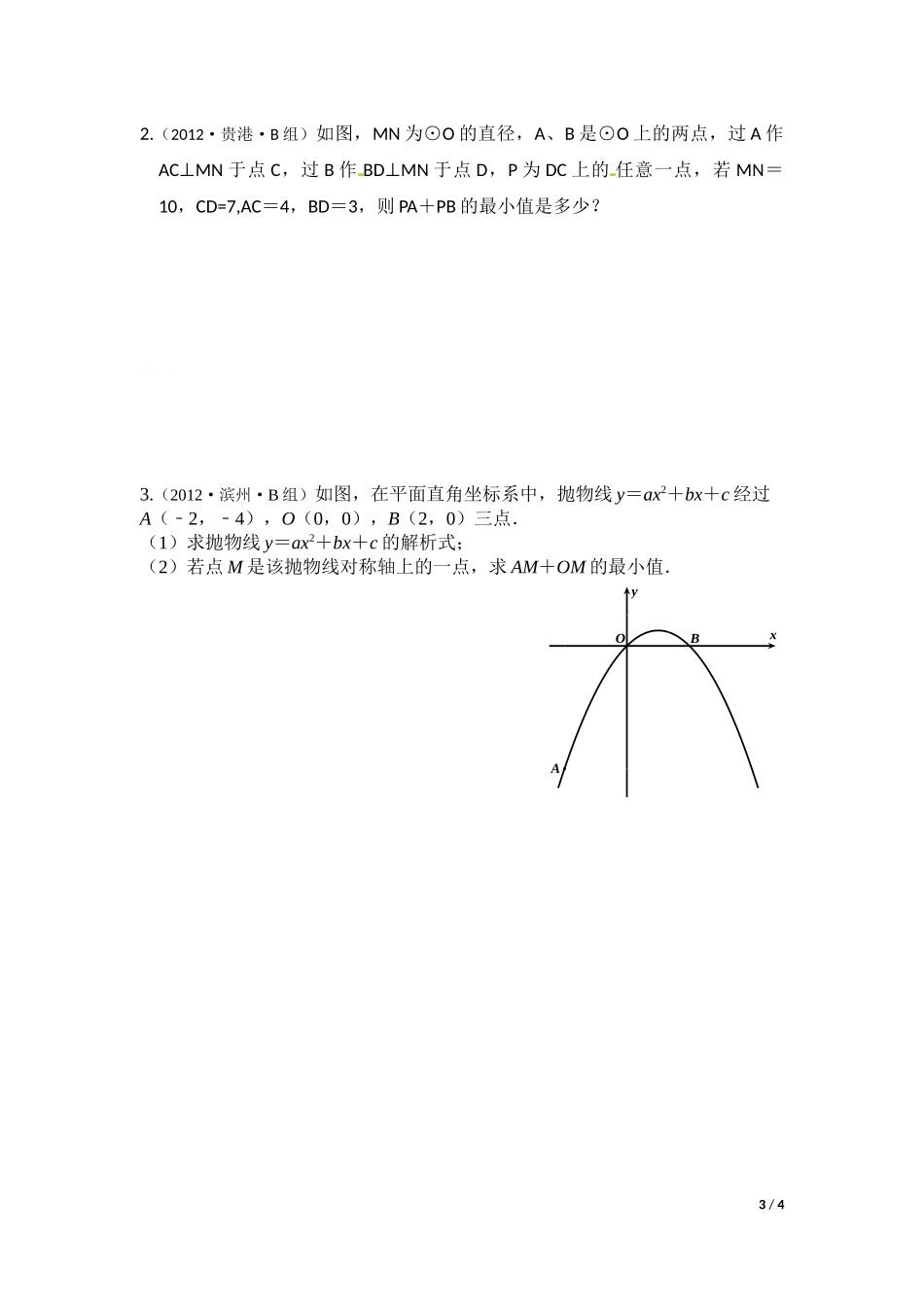
轴对称知识在最短距离问题上的应用教学目标:1.知识目标:在解决最短路径问题时,我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上,从而作出最短路径的方法来解决问题.2.能力目标:会用轴对称的知识解决最短距离问题。3.情感目标:距中考还有20多天时间,学生们在经历第一轮复习以后,已回忆、了解了基本知识点,但这些知识点还是零散的、杂乱无章的存储在一起的,实际分析、解题能力不强。碰到综合性强一点的题就毫无头绪,无从下手,心理上形成怕见综合题的阴影。教学重点:找点关于线的对称点,实现“折”转“直”.教学难点:对比2014年和2015年《考纲》中新增本节课是结合轴对称、菱形、正方形、圆、坐标轴、函数图象等具有轴对称性质的题目背景,来解决最短距离问题.教学过程:一.课前热身(A组)1.如图,A,B两点是直线l异侧的两定点尺规作图:在直线l上确定一点p,使PA+PB的最小.理论依据:2.如图,A,B两点是直线l同侧的两定点尺规作图:在直线l上确定一点p,使PA+PB的值最小.二.典型例题例1.(2014·锦州·A组)菱形ABCD的边长为8,P在对角线BD上,且E为AB中点,∠ABC=60°,求EP+AP的最小值1/4lABlBA例2.(2012·贵港·B组·改编)如图,过A作ACMN⊥于点C,过B作BDMN⊥于点D,P为DC上的任意一点,若DC=14,AC=8,BD=6,则PA+PB的最小值是三.巩固提高1.(2014·宿迁·A组)正方形ABCD的边长为8,P在对角线BD上,且E为AB中点,求EP+AP的最小值.2/4CDMNBAEABDCEBCAD2.(2012·贵港·B组)如图,MN为⊙O的直径,A、B是⊙O上的两点,过A作ACMN⊥于点C,过B作BDMN⊥于点D,P为DC上的任意一点,若MN=10,CD=7,AC=4,BD=3,则PA+PB的最小值是多少?解法1:3.(2012·滨州·B组)如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(﹣2,﹣4),O(0,0),B(2,0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M是该抛物线对称轴上的一点,求AM+OM的最小值.3/4yxABO小测:(限时10分钟):学号:姓名:1.(2013·汕头·B组)已知二次函数y=x2-2mx+m2-1.(1)如图,当m=2时,该抛物线与y轴交于点C,顶点为D,求C、D两点的坐标;(2)在(1)的条件下,x轴上是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.4/4yxDCO