28.1锐角三角函数2VIP免费

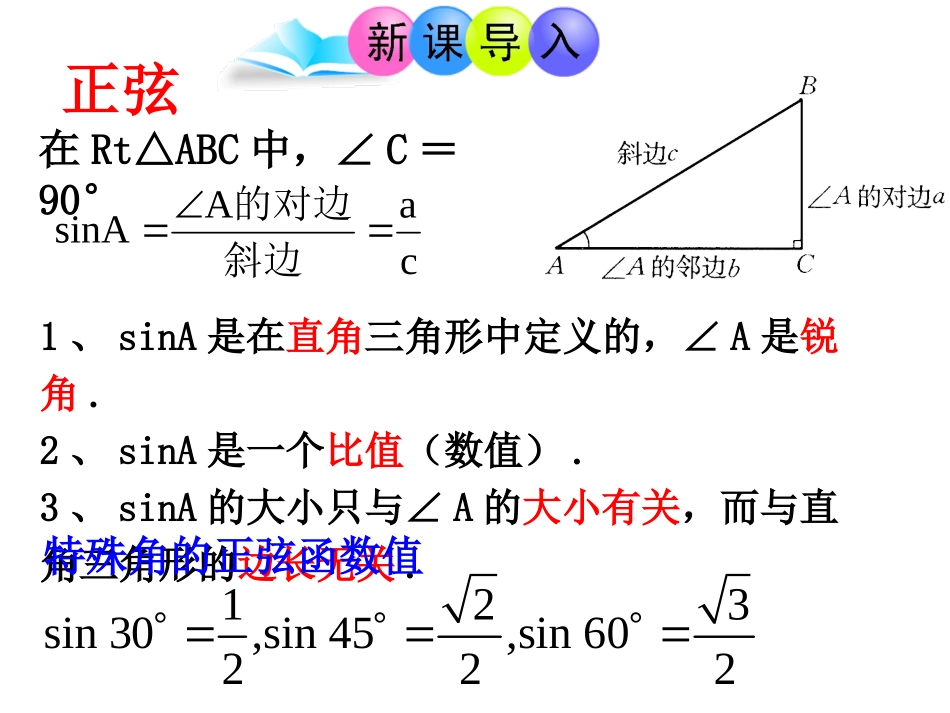
ABCcba┌28.1锐角三角函数第2课时1、理解余弦、正切的概念；2、培养学生观察、比较、分析、概括的思维能力.1、sinA是在直角三角形中定义的，∠A是锐角.2、sinA是一个比值（数值）.3、sinA的大小只与∠A的大小有关，而与直角三角形的边长无关.在Rt△ABC中，∠C＝90°123sin30,sin45,sin60222特殊角的正弦函数值正弦caAsinA斜边的对边∟对边a斜边c邻边b我们把∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cbAcos斜边的邻边AbaAAtan的邻边的对边A把∠A的对边与邻边的比叫做∠A的正切，记作tanA，即ACB如图：在Rt△ABC中，∠C＝90°，∟BACbca斜边角A的对边角A的邻边对于锐角A的每一个值，sinA有唯一的值和它对应，所以sinA是A的函数，同样地，cosA，tanA也是A的函数.锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.例2如图，在Rt△ABC中，∠C＝90°，AB=10，BC＝6，求sinA、cosA、tanA的值．解：∵ABBCAsin63sin105BCAAB又86102222BCABAC,54cosABACA3tan4BCAACABC6101.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值．解：由勾股定理222213125BCABACABC13125sin13BCAAB12cos13ACAAB5tan12BCAAC5cos13BCBAB12tan5ACBBC如图，在Rt△ABC中，∠C=90°，BC=6，sinA=，求cosA，tanB的值.ABC6解：2222ACABBC1068又，53BCsinA,ABBC5AB610sinA3，AC4AC4cosA,tanB.AB5BC3如图，在Rt△ABC中，∠C＝90°，AC＝8，tanA＝，求：sinA、cosB的值．43ABC8解：3tan4BCAAC8AC338644BCAC63sin105BCAAB22228610ABACBC63cos105BCBAB如图，已知AB是半圆O的直径，弦AD、BC相交于点P，若DPB,那么()CDAB1.sin,.cos,.tan,.tanABCDB变式：如图，已知AB是半圆O的直径，弦AD、BC相交于点P，若AB=10，CD=6，求.sinOCDBAP4sin5如图，在Rt△ABC中，∠C＝90°，cosA＝，求sinA、tanA的值．1517解：∵15cos17ACAAB88sin,1717BCkAABk88tan1515BCkAACkABC设AC=15k，则AB=17k∴2222(17)(15)8BCABACkkk（2010·黄冈中考）在△ABC中，∠C＝90°，sinA＝求cosB，tanB的值。45BAC如图，在Rt△ABC中，∠C＝90°(1)求证：sinA=cosB，sinB=cosA(2)求证：sintancosAAA(3)求证：22sincos1AAABC1、如图,在Rt△ABC中,锐角A的邻边和斜边同时扩大100倍,tanA的值（）A.扩大100倍B.缩小100倍C.不变D.不能确定ABCC2、下图中∠ACB=90°，CD⊥AB,垂足为D.指出∠A和∠B的对边、邻边.ABCDCD1tanAAC()()CD2tanBBC()BCACBDAD1.（2011·湖州中考）如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的值为()A.2B．C．D．【解析】选B.根据正切的函数定义，角A的正切应是它的对边与邻边的比，所以B是正确，A是∠B的正切；C和D都错．5555212在Rt△ABC中AasinAAc的对边的斜边AbcosAAc的的邻边的的斜边AatanAAb的的对边的的邻边定义中应该注意的几个问题:回味无穷1、sinA、cosA、tanA是在直角三角形中定义的，∠A是锐角(注意数形结合，构造直角三角形)。2、sinA、cosA、tanA是一个比值（数值）。3、sinA、cosA、tanA的大小只与∠A的大小有关，而与直角三角形的边长无关。