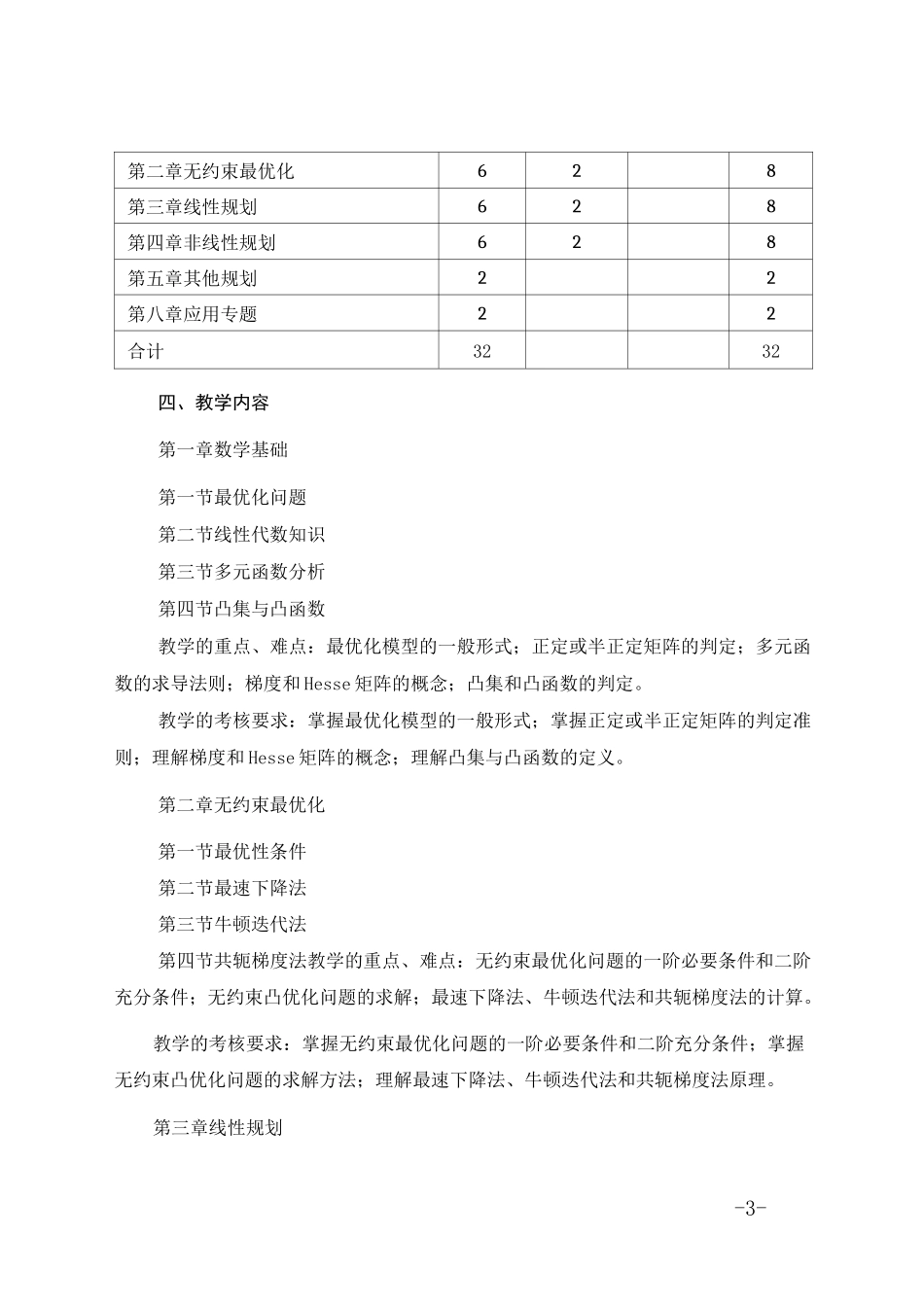
-1-最优化理论》教学大纲课程编号:112302A课程类型:专业选修课总学时:32讲课学时:26实验学时:6学分:2适用对象:金融工程专业先修课程:数学分析、线性代数、经济学、金融学一、教学目标最优化问题即在有限种或无限种可行方案(决策)中选择最优的方案(决策),与之相对应的最优化理论是数学领域的一个重要分支,也是金融工程专业学生需要掌握的必备工具之一。现代金融学研究的技术化程度日益增加,金融工程的许多问题都与最优化理论与方法密切相关,例如:投资组合选择与资产配置、期权的定价与对冲、金融风险的度量与管理、资产和负债的现金流管理等等。本课程拟对最优化的基础理论和求解方法进行一个比较全面和系统的介绍,其中涉及到的方法包括:线性规划、非线性规划、二次规划、锥优化、整数规划、动态规划、随机规划等等。通过本课程的学习,实现以下几个教学目标:目标1:帮助学生了解各类最优化模型的数学理论与求解方法;目标2:使学生理解如何应用这些优化模型分析经济学和金融学相关问题。二、教学内容及其与毕业要求的对应关系本课程主要介绍几种主要的最优化模型的理论与方法,根据最优化模型的类别进行划分,分为无约束最优化和有约束最优化两大类别。其中,无约束最优化问题的-2-子类别较少、难度相对较低,主要从理论方法和数值方法两方面进行讲解;有约束最优化重点讲解线性规划的单纯形法和非线性规划的库恩塔克条件,在时间允许的情况适当介绍其他类别的高级规划课题。基本教学内容的框架图如下:本课以课堂讲授为主,间之以案例教学、随堂练习和课后作业,针对适当的问题讲解其计算机程序实现,使学生既能掌握理论,也能动手操作,切实做到理论与实践相结合。该课程旨在进一步完善金融工程专业学生的数理知识,一方面有利于强化与完善了金融专业学生的数理知识体系,同时结合经济学和金融学实际问题进行讲解学习,锻炼了学生们思考学习的能力,更训练了学生应用数理思维分析经济金融问题的能力,与金融工程专业学生的毕业要求相呼应。三、各教学环节学时分配教学课时分配章节内容讲课实验其它合计第一章数学基础44-3-第二章无约束最优化628第三章线性规划628第四章非线性规划628第五章其他规划22第八章应用专题22合计3232四、教学内容第一章数学基础第一节最优化问题第二节线性代数知识第三节多元函数分析第四节凸集与凸函数教学的重点、难点:最优化模型的一般形式;正定或半正定矩阵的判定;多元函数的求导法则;梯度和Hesse矩阵的概念;凸集和凸函数的判定。教学的考核要求:掌握最优化模型的一般形式;掌握正定或半正定矩阵的判定准则;理解梯度和Hesse矩阵的概念;理解凸集与凸函数的定义。第二章无约束最优化第一节最优性条件第二节最速下降法第三节牛顿迭代法第四节共轭梯度法教学的重点、难点:无约束最优化问题的一阶必要条件和二阶充分条件;无约束凸优化问题的求解;最速下降法、牛顿迭代法和共轭梯度法的计算。教学的考核要求:掌握无约束最优化问题的一阶必要条件和二阶充分条件;掌握无约束凸优化问题的求解方法;理解最速下降法、牛顿迭代法和共轭梯度法原理。第三章线性规划-4-第一节LP问题的基本性质第二节单纯形法第三节对偶理论第四节灵敏度分析教学的重点、难点:线性规划的标准型转化;可行解、基本解和最优解之间的关系;利用单纯形法求解线性规划问题;两阶段法和大M法;对偶理论和灵敏度分析。教学的考核要求:掌握问题的基本性质,掌握线性规划的标准型转化准则;能够运用单纯形法求解线性规划问题;理解对偶理论,了解灵敏度分析。第四章非线性规划第一节拉格朗日方法第二节库恩塔克条件第三节凸规划的最优性条件第四节罚函数方法教学的重点、难点:等式约束的拉格朗日方法;不等式约束的库恩塔克条件;凸规划的最优性条件;外罚函数法和内罚函数法。教学的考核要求:掌握拉格朗日算法的一般方法;理解库恩塔克条件;理解凸规划的最优性条件;了解两种罚函数方法。第五章其他规划第一节整数规划第二节动态规划第三节随机规划教学的重点、难点:整数规划的分支定界法;动态规划的顺序递归和逆序递归;随机规划的理论和算法。...