圆的切线复习111VIP免费

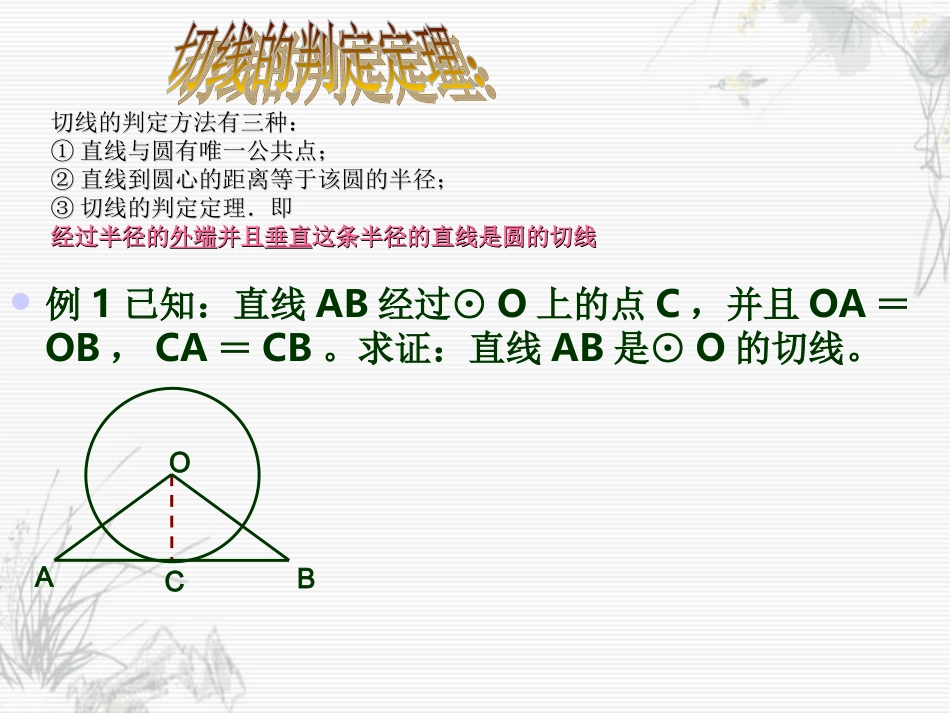
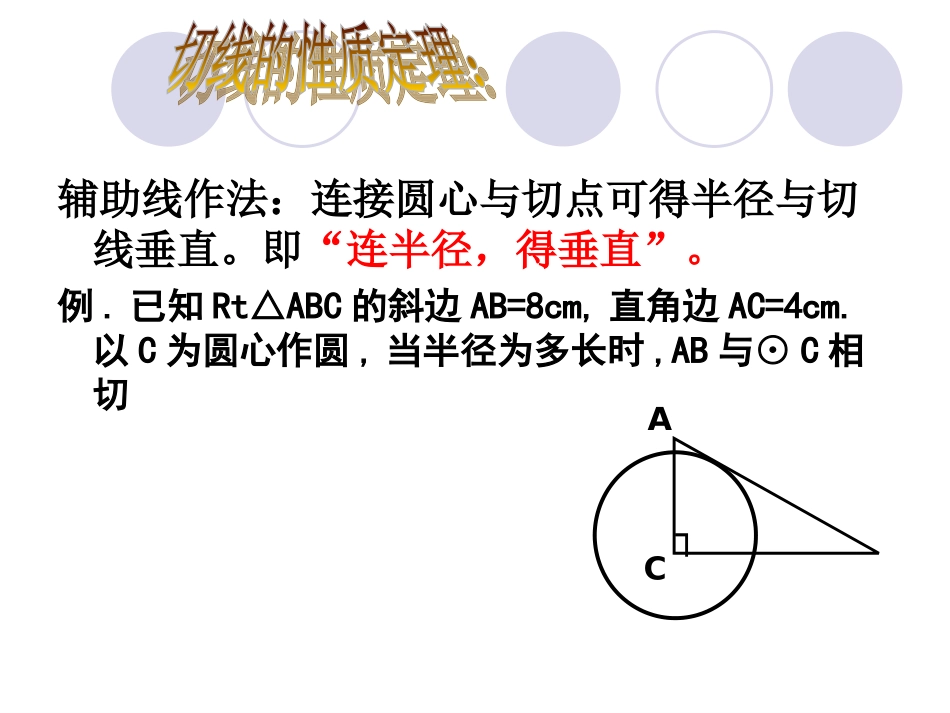
例1已知：直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB。求证：直线AB是⊙O的切线。OCBA切线的判定方法有三种：切线的判定方法有三种：①①直线与圆有唯一公共点；直线与圆有唯一公共点；②②直线到圆心的距离等于该圆的半径；直线到圆心的距离等于该圆的半径；③③切线的判定定理．即切线的判定定理．即经过半径的经过半径的外端外端并且并且垂直垂直这条半径的直线是圆的切线这条半径的直线是圆的切线辅助线作法：连接圆心与切点可得半径与切线垂直。即“连半径，得垂直”。例.已知Rt△ABC的斜边AB=8cm,直角边AC=4cm.以C为圆心作圆,当半径为多长时,AB与⊙C相切AC┐从圆外一点引圆的两条切线，它们的切线长相等；这点与圆心的连线平分这两条切线的夹角。BAPO．．．∵PA、PB为⊙O的切线∴PA=PB,∠APO=BPO∠练习１如图,⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少？AOBP练习2如图：PA,PC分别切圆O于点A,C两点,B为圆O上与A,C不重合的点,若∠P=50°,则∠ABC=___OCPAB2.已知:如图,O⊙交OA于C,弦BC＝AC,A∠＝30°求证：AB是⊙C的切线OBAC（6）1.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB和CD相等,且AB与小圆相切于E求证：CD与小圆相切EFOABCD.(5)3、已知：AB是圆O的直径，C是AB延长线上的一点，CD切圆O于点D，DE⊥AB于点E。求证：∠CDB=∠EDBEACODBOCBADE12344.如图RTABC△中,C=90∠0,以AC为直径的⊙O交斜边AB于D,OEAB∥交BC于E求证:DE是圆O的切线证明：连结OD∵OE∥AB,∴∠1＝∠2，∠3＝∠4，又∵OA=OD,∴∠1=∠3.∴∠2=∠4在△OCE和△ODE中OC=OD，∠2＝∠4，OE=OE∴△OCE≌△ODE.∵∠C=∠900∴∠ODE=900,即DE⊥OD.∴DE是⊙O的切线。5、如△ABC中∠C90﹦0,AC＝12cm,BC=16cm⊙O的直径MN在AB上,且分别切AC于D,BC于E求MN的长解：连结OD，OE,设圆的半径为R.∵⊙O分别切AC,BC于E，∴OD＝OE=R,ODAC,OEBC,⊥⊥又∵∠C90﹦0，∴DC=OE=R,ODBC.∥∴﹦,即.解得，Rcm.﹦∴MN=cm.ODBCADACR1612-R12487967BCAONMDE方法小结：根据切线的性质，构造相似三角形利用相似三角形对应边成比例的性质,建立方程求解。6、已知,如图,D(0,1),⊙D交y轴于A、B两点,交x轴负半轴于C点,过C点的直线:y=－2x－4与y轴交于P.试猜想PC与⊙D的位置关系，并说明理由.思考：判断在直线PC上是否存在点E，使得SEOC△=4S△CDO,若存在，求出点E的坐标；若不存在，请说明理由.解：令x=0，得y=-4;令y=0,得x=-2∴C(-2,0),P(0,-4)又∵D(0,1)∴OC=2,OP=4,OD=1,DP=5在RtCOD△中,CD2=OC2+OD2=4+1=5在RtCOP△中,CP2=OC2+OP2=4+16=20在△CPD中,CD2+CP2=5+20=25,DP2=25∴CD2+CP2=DP2∴△CDP为直角三角形,且∠DCP=90°∴PC为⊙D的切线.直线y=-2x-4PC是⊙O的切线，理由如下：解：假设在直线PC上存在这样的点E(x0,y0),使得SEOC△=4S△CDO，1122121ΔCODODCDS4210yCDSEOC40y40y∵E点在直线PC：y=-2x-4上，∴当y0=4时有：442x4x当y0=-4时有：442x0x∴在直线PC上存在满足条件的E点，其的坐标为(-4,4),(0,-4).2.根据切线的性质,构造相似三角形,利用相似三角形对应边成比例的性质,建立方程求解,是圆的计算中常用的一种方法。(如例3）1.证明直线和圆的相切的基本思路：已知半径-------直接证直线与半径垂直；没有半径-----有公共点------“连半径,证垂直”(如例1）无公共点------“作垂线,证半径”（如例2）