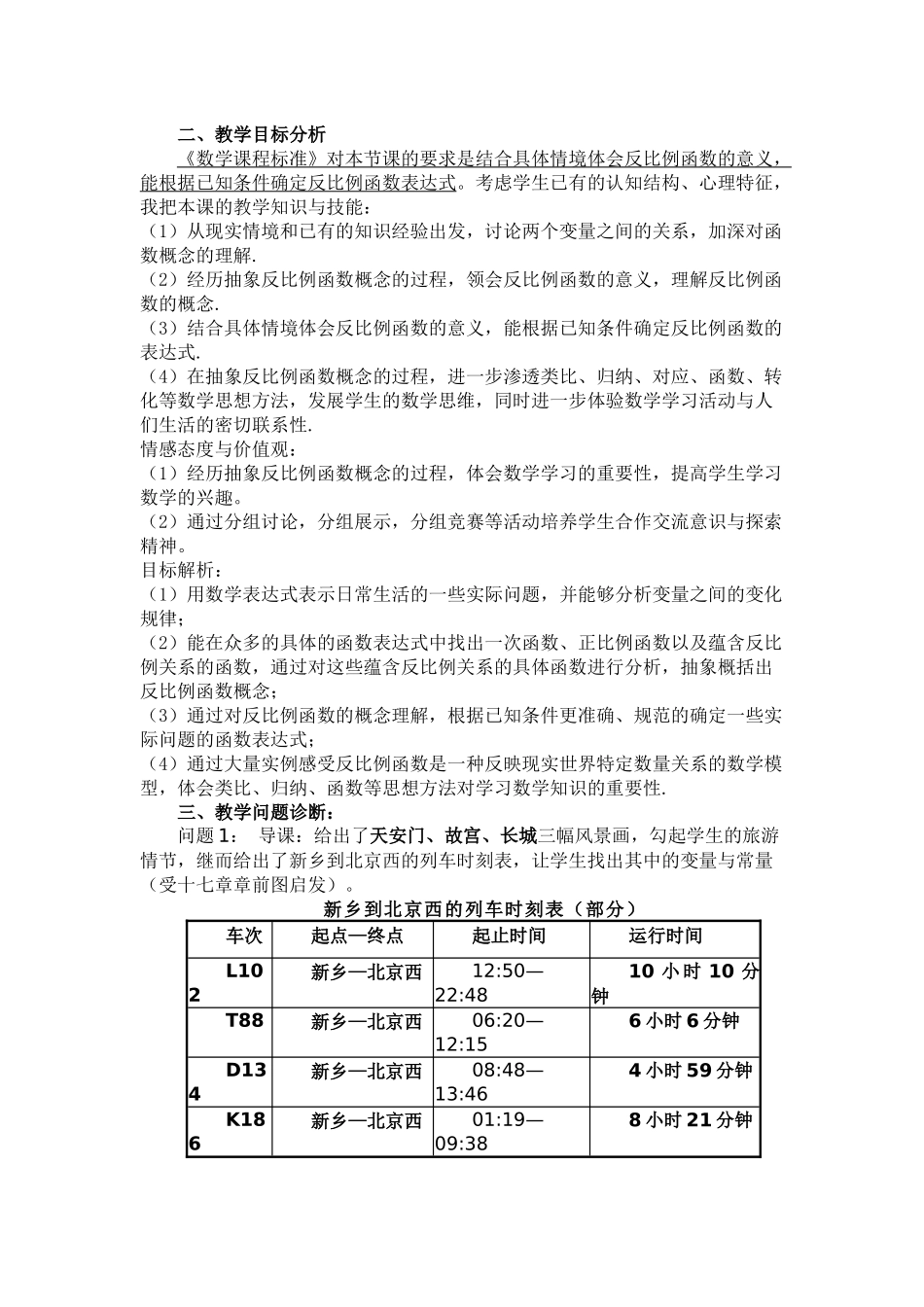
反比例函数的意义教学设计说明长垣邵艳星一、教材分析1.内容分析:本节课是“反比例函数”的第一节课,是继正比例函数、一次函数之后,二次函数之前的又一类型函数,启着承上启下的作用,本节课主要通过丰富的生活事例,让学生归纳出反比例函数的概念,并进一步体会函数是刻画变量之间关系的数学模型,从中体会函数的模型思想。因此本节课重点是理解和领悟反比例函数的概念与用代定系数法求反比例关系式,所渗透的数学思想方法有:类比,转化,建模。本节课对学习后面反比例函数的图像和性质及反比例函数与实际问题,有重要的意义,同时,也是对八年级上册,一次函数,正比例函数的进一步延伸与拓展。2.学情分析:对八年级学生来说,虽然他们已经对函数,正比例函数,一次函数的概念、图象、性质以及应用有所掌握,但他们面对新的反比例函数时,还可能存在一些思维障碍,如学生不能准确地找出变量之间的自变量和因变量,以及如何从事例中领悟和总结出反比例函数的概念,因此,本节课的难点是理解和领悟反比例函数的概念。3.地位分析:生活中处处存在着反比例函数的事例,更好的阐释数学来源于生活,服务着生活;在初中阶段所有函数中起着承上启下的作用,使学生的知识更具连贯性,系统性;在中招考试中的重要性,近三年所占分值为:2012年3分、2011年12分、2010年10分。设计理念分析:使学生理解反比例的概念并能用函数的方法表示生活中的一些变化过程,通过问题情景,引导学生运用归纳法写出表示现实生活中的一些变化过程的函数关系式,培养学生解决实际问题的意识和能力,通过从实际生活问题中归纳出数学知识,然后运用数学知识解决实际问题这一过程,很好地调动学生学习数学的积极性,让他们明白学习“生活中有数学,学习有用的数学”的道理。二、教学目标分析《数学课程标准》对本节课的要求是结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数表达式。考虑学生已有的认知结构、心理特征,我把本课的教学知识与技能:(1)从现实情境和已有的知识经验出发,讨论两个变量之间的关系,加深对函数概念的理解.(2)经历抽象反比例函数概念的过程,领会反比例函数的意义,理解反比例函数的概念.(3)结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数的表达式.(4)在抽象反比例函数概念的过程,进一步渗透类比、归纳、对应、函数、转化等数学思想方法,发展学生的数学思维,同时进一步体验数学学习活动与人们生活的密切联系性.情感态度与价值观:(1)经历抽象反比例函数概念的过程,体会数学学习的重要性,提高学生学习数学的兴趣。(2)通过分组讨论,分组展示,分组竞赛等活动培养学生合作交流意识与探索精神。目标解析:(1)用数学表达式表示日常生活的一些实际问题,并能够分析变量之间的变化规律;(2)能在众多的具体的函数表达式中找出一次函数、正比例函数以及蕴含反比例关系的函数,通过对这些蕴含反比例关系的具体函数进行分析,抽象概括出反比例函数概念;(3)通过对反比例函数的概念理解,根据已知条件更准确、规范的确定一些实际问题的函数表达式;(4)通过大量实例感受反比例函数是一种反映现实世界特定数量关系的数学模型,体会类比、归纳、函数等思想方法对学习数学知识的重要性.三、教学问题诊断:问题1:导课:给出了天安门、故宫、长城三幅风景画,勾起学生的旅游情节,继而给出了新乡到北京西的列车时刻表,让学生找出其中的变量与常量(受十七章章前图启发)。新乡到北京西的列车时刻表(部分)车次起点—终点起止时间运行时间L102新乡—北京西12:50—22:4810小时10分钟T88新乡—北京西06:20—12:156小时6分钟D134新乡—北京西08:48—13:464小时59分钟K186新乡—北京西01:19—09:388小时21分钟诊断:目的是让学生先从图中找出变量与常量,继而引出反比例关系。可能出现的问题有,学生把车次与起止时间与变量混为一谈,而忽略了隐藏的变量速度;找到了时间、速度与路程和等量关系,没能提炼出来反比例关系,偏离了导课的目的。应对措施:首先让学生做好预习,结合课本内容明确本节课的大致学习目标与内容;然后在引导时说明...